-
Свежие записи
Рубрики
- Анекдоты (512)
- Афоризмы (12)
- Всякое-разное (15)
- Демотиваторы (11)
- Прикольное и смешное видео (20)
- Прикольные истории (8)
- Прикольные картинки (47)
- Прикольные стишки (44)
- Прикольные фотки (18)
- Просто шутки (71)
Приглашаю присоединиться ко мне в следующих сервисах:
Второй закон термодинамики в различных формулировках
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Анекдот второй закон термодинамики
"Бомбы стремятся лететь туда, где нефть дешевле".
Второй закон политической термодинамики: "Бомбы стремятся лететь туда, где нефть дешевле".
По теме:
Законы Вселенной:
ЗАКОН БИОМЕХАНИКИ:
Как только вы, работая над авто в гараже, запачкаете руки солидолом, вам приспичит в туалет.
ЗАКОН ПРИЧИНО-СЛЕДСТВЕННОЙ СВЯЗИ:
Если вы наплетете боссу, что вы опоздали на работу по причиние проколотого колеса, то завтра на пути на работу вы действительно проколете колесо.
ЗАКОН ДВИЖЕНИЯ ТЕЛ:
Если вы перестроитесь в другой поток движения, тот из которого вы перестроились сразу начнет двигаться быстрее того куда вы перестроились.
ЗАКОН ПОГРУЖЕНИЯ ТЕЛ:
Тело, опущенное в ванну, вызывает телефонный звонок из соседней комнате.
ОБЩИЙ ЗАКОН МЕХАНИКИ:
Когда вы доказываете кому-то почему что-либо не работает, оно как раз начинает работать.
ЗАКОН БИОМЕХАНИКИ:
Сила чесотки прямо пропорциональна трудности достать до чешущегося места.
ЗАКОН ЦЕНТРОБЕЖНОСТИ:
В кинотеатре люди, наиболее близкие к центру ряда сидений, приходят последними.
ЗАКОН ТЕРМОДИНАМИКИ:
Как только вы в офисе нальете кружку горячего кофе, вас вызовет босс, и продержит до тех пор, пока кофе не остынет.
ЗАКОН БЛИЗОСТИ:
Если в раздевалке, состоящей из 500 узких шкафчиков, всего двое людей, их шкафчики будут рядом друг с другом.
ЗАКОН ПАДАЮЩИХ ТЕЛ:
Шансы бутерброда с повидлом на падение повидлом вниз прямо пропорциональны стоимости ковра.
ЗАКОН ЛОГИКИ:
Босс заявляет, что возможно все, если делать это придется не ему.
Идет бомж по помойкам академгородка.
Видит — женщина голая лежит. Он подходит к ней и спрашивает: "Второй закон термодинамики? " Она отвечает: "Энтропия изолированной системы не может уменьшаться". Бомж идет дальше и думает: "Нормальная баба! И чего выбросили? "
— Допрыгался. Я ВСЁ знаю.
— Господи! Неужели?
— Да! Абсолютно ВСЁ!
— Второй закон термодинамики?
— ...
— Ты ж моя лживенькая истеричка.
— Допрыгался. Я ВСЁ знаю.
— Господи! Неужели?
— Да! Абсолютно ВСЁ!
— Второй закон термодинамики?
— ...
— Ты ж моя лживенькая истеричка.
Сначала подставили Клинтона Моникой, Берлускони обвиняли в многочисленных
связях с женщинами, потом посадили Стросс-Кана за горничную… Как видите,
господа, натуралов гонят из мировой политической элиты.
— А вот я вижу в политической жизни России необычайное оживление.
— ?
— Раньше на роль придворного шута претендовал только Владимир Вольфович, а сейчас там целая очередь.
Пропасть между народом и политической "элитой" становится настолько глубокой, что можно придумать любую небылицу, например, что Дума ввела налог на нижнее белье, и люди поверят. Но, что самое печальное, нельзя быть на 100% уверенным, что это выдумка со временем не воплотится в жизнь...
Первый закон кота: случайно проснулся — поешь!
Второй закон кота: спи чутко!
Едут в машине в Москву лица кавказской национальности. На КПП их останавливает мент:
— Вот, мужики, закон вышел, что лицам кавказской национальности необходимо сдать ведро спермы... Вот вам ведерко, вот лесочек, идите и дрочите...
Ну, те пошли... через 20 минут приносят ведерко — а там все на дне.
— Ну нет, ребята... вот, смотрите, бумага с печатью, закон, понимаете, такой... идите, продолжайте...
И те пошли снова. Через два часа приносят полведра, уже на коленях стоят, просят пощадить. Но мент непреклонен: надо полное ведро.
Уже ночью припозают едва живые с полным ведром.
— Вот это другое дело. Езжайте с Богом...
Уезжают. Мент берет ведерко, подходит к канаве (а там уже полно спермы), выливает, напевая: "Любимый город может спать спокойно".
Издал лев, царь зверей, закон значит:
- Каждый день все зверье должно приносить мне мясо. Кто этого делать не будет - получит #%ем по лбу!
День первый. Приносит заяц сумку. Лев говорит:
- Сколько кило?
- Пять.
Лев сумку открывает, смотрит - там капуста.
- Ах, ты, косой обманщик!
Хлоп ему пять раз по лбу. Заяц - фрррр, улетел в кусты. Через минуту из кустов доносится душераздирающий смех. Лев заглядывает в кусты:
- Эй косой, ты чего, мало тебе, что ли?
- Да нет, ничего, просто вон ежик несет 10 килограммов яблок, а закон ты сам знаешь!
Закон о защите прав детей
У лепшего кореша две дочки близняшки. Воспитывает он их один, жена сбежала к молодому любовнику. На момент описываемых событий дочкам было лет по 13. Внешность уже фотомодельная, менталитет то же.
Сидим у него дома на кухне, курим, пьем кофе, размеренно беседуем. Стремительно распахивается входная дверь, и на пороге появляются обе наследницы, бухтят о чем то о своем, на нас ноль внимания. Сам папа довольно миролюбиво, попыхивая сигаретой, интересуется.
- Девки, ни хрена ни могу понять, в комнатах бардачина, кровати не заправлены, посуда не вымыта. За приборку, мухами, и что бы жужжало.
На что обе вертихвостки, синхронно скрестив руки и наклонив головы, выдали.
- Ты не имеешь права нас заставлять что-то делать. Нам в школе сказали что есть закон о защите прав детей, там это написано.
Повисла пауза. Миролюбивое настроение папы куда-то пропало. Он требовательно постучал по краю стола.
- Так, прошмандовки, положили сюда ваши дорогие мобильники, живо положили, я сказал. Нет в этом законе такого, что бы я по пятнашке вам телефоны покупал. И интернета у вас не будет. Да и незачем он вам, компы я тоже отберу. Ни хрена точно в законе этом долбаном про компьютеры нет. Иш ты юристы, выучили их на свою голову. Про шмотки ваши забудьте, в валенках походите. В фуфайки перелезете.
Впрочем уже на интернете одна из девиц насупившись, и злобно оглядываясь мыла посуду, а со стороны комнат доносился деловой топот. В конце монолога суровый папаша улыбнулся.
- Растут дети.
И в пол голоса поинтересовался не знаю ли я продаются ли еще фуфайки.
Депутаты ГосДумы приняли закон о порядке сбора пчёлами нектара и изготовлении пчёлами мёда, а также закон о регулировке внутреннего распорядка жизни в ульях.
- Билетик предъявите!
- Да вы что! Я же проводник!
- Да хоть конденсатор, закон есть закон.
2016 год. Госдума обсуждает запрет ловли покемонов.
2017 год. В госдуме принимают закон регламентирующий ловлю покемонов.
2018 год. Обсуждается закон о закупке редких покемонов для депутатов и их семей.
2016 год. Госдума обсуждает запрет ловли покемонов.
2017 год. В госдуме принимают закон регламентирующий ловлю покемонов.
2018 год. Обсуждается закон о закупке редких покемонов для депутатов и их семей.
Хорошо, чтобы у нас, как в одной из областей древней Греции, существовал такой обычай — когда сенатор предлагал в новый закон, он делал это на повозке с веревкой на шее. Если закон принимался — убирали веревку, если нет — повозку.
Настоящим предлагается внести изменения в один из базовых физических законов — закон сохранения материи.
Теперь он должен выглядеть примерно так:
"Если где-то чего-то убавилось, то в другом месте этого же должно прибавиться в том же количестве. За исключением авторучек."
В такой редакции закон должен существовать до тех пор, пока учеными не будет обнаружено место куда, блин, постоянно деваются все авторучки
Один мужик идет вдоль улицы и копает ямы, за ним второй эти ямы закапывает. Прохожий удивляется:
- Вы что делаете, идиоты? Один копает, второй закапывает?
- Я не второй, я третий. Второй не вышел на работу, он должен был деревья сажать.
Второй закон Архимеда гласит:
"Жидкость, погруженная в тело, через семь лет пойдет в школу"
Встречаются два профессора математики.
Первый, вздыхая:
- Коллега, а ведь меня опять обокрали!
Второй:
- Представьте себе, коллега, я раз и навсегда решил эту проблему!
Первый:
- Хм... интересно было бы узнать, как?
Второй:
- Я использовал теорию вероятности и поставил на свою дверь шесть
самых дешевых китайских замков!
Первый:
- Ну и при чем тут теория вероятности, если их всех можно открыть
одним ключом?!
Второй:
- Не скажите, коллега! Когда я выхожу из дома, я три замка закрываю,
а три - нет!..
Второй закон термодинамики
Согласно закону сохранения энергии в случае определенных процессов, объем используемой энергии остается неизменным. Для того, чтобы объяснить как энергия может превращаться можно обратиться к понятию второй закон термодинамики. Данный закон подтверждает необратимость некоторых явлений в природе и указывает траекторию энергетических изменений внутри определенных процессов. Закон был сформулирован на основе наблюдений за происходящее в природе, что позволило понять сущность и характер протекания определенных явлений. Все законы физики основаны на опытах и наблюдениях и позволили формулировать определенные заявления на основе происходящего в природе.
В качестве основы для второго закона термодинамики стали необратимые и непроизвольные процессы, которые происходят исключительно в одно направление и/или без постороннего внешнего воздействия. Классические примеры таких процессов это старение, смерть. Без того чтобы обобщать, можно обратиться к более простым процессам: духи распространяются очень быстро при распылении, а обратному соединению они не подаются; также легко превратить яйца в омлет, так что обратно в скорлупу их невозможно вернуть.
Закон работает в изолированных системах, но также может восприниматься как рабочим в случае систем, у которых есть возможность получить тепло извне. В подобных системах энтропия будет расти даже быстрее. Показатель энтропии указывает на систему с характером неупорядоченности, то есть сама энтропия и есть мера беспорядка. Высокий показатель энтропии это высокий уровень хаотичности движения частиц внутри системы. Классический пример этого состояния это превращение льда в воду и его невозможность стать снова льдом самостоятельно. В случае превращения воды в лед должно происходить понижение уровня энтропии.
Говоря о том, что такое термодинамика второй закон необходимо вспомнить, что собой представляет первый закон термодинамики. Он олицетворение всех известных процессов в природе и соблюдается с 100% точностью. Все что может противоречить этому закону, в природе не существует. Данный закон ничего не отрицает, но и не утверждает, а в качестве вспомогательного элемента для разъяснения определенных процессов вступает второй закон термодинамики, всем известный в разных формулировках. Невзирая на то, что закон простой, он часто интерпретируется некорректно.
Второй закон термодинамики появился, как необходимость определить направление физических процессов определенные первым законом. В первую очередь необходимо отметить, что разные виды энергии обладают различной способностью перевоплощаться в другую энергию. Существует ограничение, которое не позволяет внутренней энергии стать механической энергии и это разъясняется законами термодинамики.
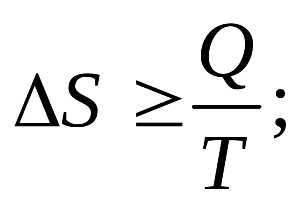
Второй закон термодинамики в различных формулировках
Существует несколько формулировок данного закона, которые объясняют одну правду различными способами. Первый кто сформулировал его это Р. Клаузиус, после последовали формулировки Томсона, Больцмана, Кельвина. Наличие различных интерпретации данного закона позволяет его понять лучше. Поэтому будет не лишним ознакомиться с каждым из них.
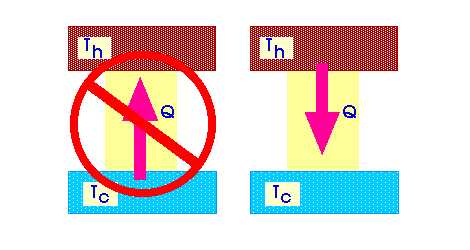
1. Переход тепла от тела с невысокой температурой к другому телу с более высоким уровнем температуры невозможен. (Клаузиус)
2. Любой процесс является невозможным, если для его осуществления должно использоваться тепло взятое от постороннего тела. (Томсон)
3. Состояние энтропии не может стать меньше в полностью закрытых системах, которые не получают никакую внешнюю энергию. (Больцман)
4. Периодические процессы, происходящие исключительно за счет теплоты единого источника являются невозможными. Создание вечного теплового двигателя, который совершал бы механические процессы за счет потери тепла любого тела, является невозможным. (Кельвин).
Согласно всем формулировкам можно условно определить, что процессы можно называть необратимыми, если механическая энергия проходит путь модификации во внутренней энергии при наличии процесса трения. Отсутствие параметра трение позволило бы в ином случае получать обратное протекание процессов. Обратные процессы можно считать абстрактными с учетом того, что протекают они, как правило, в присутствии реакции теплообмена и трения.
Второй закон термодинамики формулы
Существуют определенные уравнения, которые помогают рассматривать второй закон термодинамики согласно более конкретным данным. Основное уравнение это уравнение Больцмана, которое позволяет вычислять параметр энтропия.
S = Q/ T
С целью понять, что собой представляет параметр энтропия можно рассмотреть пример с системой, в которой два тела с не одинаковой температурой будут обмениваться теплом, пока температура обоих тел не сравнится. Тепло будет передаваться исключительно от тела с температурой выше к более холодному. Тело, которое отдает тепло, получает пониженный уровень энтропии, только не по тем параметрам, по которым увеличиться энтропия тела, получившее это тепло. Энтропия обеих тел по итогам после процесса передачи тепла будет выше для всей системы. Это указывает, что данная величина стремиться к энному максимуму для всех закрытых систем. Также неопровержимо заявление относительно того, что действие по передаче тепла будет продолжать происходить самопроизвольно, пока будут существовать перепады температуры.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Первое начало термодинамики — Википедия
Пе́рвое нача́ло термодина́мики (первый закон термодинамики) — один из основных законов этой дисциплины, представляющий собой конкретизацию общефизического закона сохранения энергии для термодинамических систем, в которых необходимо учитывать термические, массообменные и химические процессы[1][2][3]. В форме закона сохранения (уравнения баланса энергии) первое начало используют в термодинамике потока и в неравновесной термодинамике. В равновесной термодинамике под первым законом термодинамики обычно подразумевают одно из следствий закона сохранения энергии, из чего проистекает отсутствие единообразия формулировок первого начала, используемых в учебной и научной литературе (К. А. Путилов в своей монографии[4] приводит шесть формулировок, которые он считает наиболее удачными).
Первое начало термодинамики было сформулировано в середине XIX века в результате работ немецкого учёного Ю. Р. Майера, распространившего закон сохранения механической энергии сначала на термические (1842), а затем (1845) и на все немеханические явления, английского физика Дж. П. Джоуля (1843), экспериментально обосновавшего новый закон, и немецкого физика Г. Гельмгольца (1847), который — не зная о работах Майера — распространил закон сохранения энергии на все её виды и сыграл решающую роль в том, что этот закон стал общепризнанным[5].
Особенности различных формулировок первого начала термодинамики[править | править код]
Первое начало термодинамики часто формулируют как невозможность существования вечного двигателя (перпетуум мобиле) первого рода, который совершал бы работу, не черпая энергию из какого-либо источника[1][2][3]. Связь этого утверждения с законом сохранения энергии самоочевидна.
Переход от микроскопического описания системы к макроскопическому ведёт к радикальному сокращению числа физических величин, необходимых для описания системы. Поэтому в термодинамике энергетические превращения — подчас весьма сложные, — происходящие внутри системы на микроуровне, не детализирует[6], а совокупно описывают посредством специально для этой цели вводимой макроскопической величины — внутренней энергии, составной части полной энергии системы, с микроскопической точки зрения представляющей собой сумму энергий всех входящих в систему частиц[7]. По этой причине в тех учебниках, в которых не касаются вопросов термодинамики потока и неравновесной термодинамики, нередко формулируют первое начало как постулат, вводящий в физику макроскопических систем представление о внутренней энергии[2] как об аддитивной величине[8][9], являющейся однозначной, непрерывной и конечной скалярной функцией состояния термодинамической системы[10]. Как и для любой другой функции состояния, изменение внутренней энергии U{\displaystyle U} в бесконечно малом процессе есть полный дифференциал dU{\displaystyle dU}, а изменение внутренней энергии в круговом процессе равно нулю[11][12][13][14]:
| ΔU=∮dU=0.{\displaystyle \Delta U=\oint dU=0.} |
Математическое выражение, служащее дефиницией внутренней энергии, зависит от выбора термодинамических величин, используемых в качестве независимых переменных теории. Традиционно внутреннюю энергию выражают с использованием в качестве фундаментальных понятий, которым термодинамика даёт описание без дефиниций, теплоту и термодинамическую работу[1][3] (заимствуя понятие работы из других разделов физики[15][16]). Согласно Г. Кирхгофу сумма количества теплоты q{\displaystyle q} и работы w{\displaystyle w} для бесконечно малого[17]равновесного процесса[18] в закрытой системе (при использовании термодинамического правила знаков для теплоты и работы) равна изменению внутренней энергии системы в данном процессе dU{\displaystyle dU}[19][20][21][22][23]:
| dU≡q+w.{\displaystyle dU\equiv q+w.} | (Дефиниция внутренней энергии по Кирхгофу) |
Первое начало термодинамики в формулировке Кирхгофа утверждает, что существует функция состояния U{\displaystyle U}, называемая внутренней энергией и представляющая собой часть полной энергии системы, изменение которой в любом процессе в закрытой системе равно сумме работы и теплоты; каждое состояние термодинамической системы характеризуется определённым значением U{\displaystyle U}, независимо от того, каким путём система приведена в данное состояние[1][2][3]; dU{\displaystyle dU} есть полный дифференциал внутренней энергии U{\displaystyle U}[2] (величины q{\displaystyle q} и w{\displaystyle w} в общем случае есть функционалы пути, по которому совершается процесс[24][25], численные значения которых различны для различных способов проведения процесса при одинаковом исходном и конечном состояниях системы, иначе говоря, зависят от пути процесса[1][2][26]). Из первого начала в формулировке Кирхгофа вытекает, что те составные части полной энергии системы, которые не изменяются в рассматриваем процессе, во внутреннюю энергию системы не входят и, следовательно, внутренняя энергия есть изменяемая часть полной энергии системы.
Для функции состояния естественен вопрос о её аргументах. Из дефиниции Кирхгофа следует, что внутренняя энергия зависит от переменных, входящих в выражение для работы, то есть обобщённых термодинамических координат, и температуры как движущей силы теплопередачи.
Традиционно теплоту и работу трактуют как формы передачи энергии, то есть их характеризуют посредством описательных дефиниций. Именно по этой причине как математические объекты теплота и работа в дефиницию внутренней энергии по Кирхгофу входят в виде неопределяемых переменных. Давать дефиницию фундаментальной физической величине — энергии — посредством величин менее фундаментальных — теплоты и работы — есть методологический недостаток подхода Кирхгофа. Наконец, в формулировке Кирхгофа внутренняя энергия как функция состояния привязана к функциям процесса — теплоте и работе. Фактически это означает привязку внутренней энергии к равновесным процессам в закрытых системах, когда возможна однозначная трактовка понятий теплоты и работы.
Важно, что ни масса системы, ни массы (количества) составляющих систему веществ не относятся к обобщённым термодинамическим координатам, а поэтому в традиционном подходе к обоснованию термодинамики массы (количества) веществ не входят в перечень переменных, от которых зависит внутренняя энергия (или, что то же самое, масса является адиабатно заторможенной величиной[27]). Из аддитивности внутренней энергии вытекает, однако, что для флюидов (газов и жидкостей) внутренняя энергия обладает свойством экстенсивности, то есть внутренняя энергия однородной системы пропорциональна массе этой системы. Если же учесть, что масса системы равна сумме масс составляющих систему веществ, то становится понятным, что, во-первых, массы (количества) веществ могут входить в формулы термодинамики закрытых систем, и что, во-вторых, в эти формулы (например, в выражения для удельной теплоёмкости и других удельных величин) массы (количества) веществ входят не как переменные состояния, а в качестве числовых параметров, детализирующих характеристики конкретных систем. Из сказанного следует, что термодинамическое описание открытых систем постоянного состава ничем не отличается от описания свойств закрытых систем[28].
Для открытых систем переменного состава, с которыми имеют дело в химической термодинамике, первое начало формулируют в виде аксиомы о существовании внутренней энергии как функции состояния, в перечень постулируемых свойств которой входит её функциональная зависимость от масс составляющих систему веществ[29][26][30][31]. Так, К. Каратеодори (1909) выразил первое начало термодинамики в форме утверждения о существовании внутренней энергии — составной части полной энергии системы — как функции состояния, зависящей для простых систем[32] от объёма V{\displaystyle V}, давления P{\displaystyle P}, масс составляющих систему веществ m1,m2,...,mi,...{\displaystyle m_{1},m_{2},...,m_{i},...}[33][K 1]
| U=U(P,V,{mi}){\displaystyle U=U\left(P,V,\left\{m_{i}\right\}\right)} | (Первое начало в формулировке Каратеодори) |
(выражение {mi}{\displaystyle \{m_{i}\}} есть сокращение для перечисления m1,m2,...,mi,...{\displaystyle m_{1},m_{2},...,m_{i},...}) и обладающей следующими свойствами:
- для бесконечно малого адиабатного процесса изменение внутренней энергии равно работе процесса
| dU=w;{\displaystyle dU=w;} | (Изменение внутренней энергии в адиабатном процессе) |
- количество теплоты для бесконечно малого равновесного процесса в закрытой системе согласно Клаузиусу полагают (при использовании термодинамического правила знаков для теплоты и работы) равным разности между изменением внутренней энергии системы в данном процессе и работой процесса[34][35]:
| q≡dU−w.{\displaystyle q\equiv dU-w.} | (Дефиниция теплоты по Клаузиусу — Каратеодори — Борну) |
В формулировке Каратеодори внутренняя энергия не представляет собой характеристическую функцию своих независимых переменных.
В случае открытых систем переменного состава изменение внутренней энергии вследствие изменения масс составляющих систему веществ несводимо ни к теплоте, ни к работе[29], поэтому «…для открытой системы являются беспредметными как классическая точка зрения (эквивалентность теплоты и работы), так и точка зрения Каратеодори (определение теплоты)»[27]. Формальное распространение дефиниции Кирхгофа на внутреннюю энергию открытых систем переменного состава выполняют, добавляя в выражение для дефиниции внутренней энергии ещё одно слагаемое — энергию перераспределения масс составляющих систему веществ (химическую работу[36]) z{\displaystyle z}[1][26][37]:
| dU≡q+w+z,{\displaystyle dU\equiv q+w+z,} |
однако ни практического, ни теоретического значения это выражение не имеет. Дело в том, что однозначности разделения изменения внутренней энергии на теплоту и работу в традиционном подходе к термодинамике достигают, заимствуя понятие работы из других разделов физики и используя представление об адиабатной изоляции для трактовки теплоты как энергии, передаваемая без совершения работы и без изменения масс составляющих систему веществ[38] (поскольку любая адиабатная оболочка/перегородка непроницаема для вещества). Это означает, что работа и теплота представляют собой независимо измеряемые величины[1][3], тогда как способы независимого измерения химической работы отсутствуют в традиционном подходе к построению термодинамики.
Дж. У. Гиббс в своей работе «О равновесии гетерогенных веществ» (1875—1878)[39] строит термодинамику простых открытых систем, рассматривая внутреннюю энергию как функцию энтропии S{\displaystyle S}, объёма V{\displaystyle V} и масс составляющих систему веществ m1,m2,...,mi,...{\displaystyle m_{1},m_{2},...,m_{i},...}:
| U=U(S,V,{mi}).{\displaystyle U=U\left(S,V,\left\{m_{i}\right\}\right).} | (Первое начало в формулировке Гиббса) |
Распространяя термодинамику Гиббса на сложные системы[40], внутреннюю энергию полагают функцией энтропии S{\displaystyle S}, обобщённых координат x1,x2,...,xi,...{\displaystyle x_{1},x_{2},...,x_{i},...} и масс составляющих систему веществ[41][42]:
| U=U(S,{xi},{mi}).{\displaystyle U=U\left(S,\left\{x_{i}\right\},\left\{m_{i}\right\}\right).} | (Фундаментальное уравнение Гиббса в энергетическом выражении) |
В неравновесной термодинамике выражение для первого начала термодинамики выглядит так (см. статью Неравновесная термодинамика):
- ∂e∂t+∇⋅Je=0,{\displaystyle {\frac {\partial e}{\partial t}}+\nabla \cdot {\boldsymbol {J}}^{e}=0,}
где e{\displaystyle e} — сумма плотностей кинетической и внутренней энергий, Je{\displaystyle {\boldsymbol {J}}^{e}} — поток энергии.
В научной и учебной литературе можно встретить варианты математического выражения для первого начала термодинамики, отличающиеся знаками (+{\displaystyle +} или −{\displaystyle -}) перед количеством теплоты q{\displaystyle q} и работой w{\displaystyle w}. Отличия эти связаны с соглашениями, называемыми правилами (системами) знаков для теплоты и работы. В соответствии с рекомендациями ИЮПАК для равновесного процесса в закрытой системе первое начало записывается в виде соотношения[43]
| dU=q+w.{\displaystyle dU=q+w.} | (Первое начало в термодинамической системе знаков) |
или
| ΔU=Q+W.{\displaystyle \Delta U=Q+W.} | (Первое начало в термодинамической системе знаков) |
В этих выражениях использовано правило знаков ИЮПАК (термодинамическое правило знаков) для теплоты и работы, когда знаки перед U,{\displaystyle U,} q{\displaystyle q} и w{\displaystyle w} совпадают, положительными считают теплоту, подводимую к системе и работу, совершаемую над системой, а отрицательными — теплоту, отводимую от системы и работу, совершаемую системой. Для запоминания системы знаков ИЮПАК может пригодиться «эгоистическое» мнемоническое правило: положительно то, что увеличивает внутреннюю энергию системы[44].
Правило знаков ИЮПАК для теплоты (термодинамическое правило знаков для теплоты) совпадает с принятым в технической термодинамике теплотехническим правилом знаков для теплоты[45] (знаки перед dU{\displaystyle dU} и q{\displaystyle q} в математическом выражении для первого начала одинаковы). Согласно теплотехническому правилу знаков для работы положительной считают работу, совершаемую системой, а отрицательной — работу совершаемую над системой, то есть знаки перед dU{\displaystyle dU} и w{\displaystyle w} в математическом выражении для первого начала противоположны[45]:
| dU=q−w.{\displaystyle dU=q-w.} | (Первое начало в теплотехнической системе знаков) |
В термохимическом правиле знаков для теплоты положительной считают теплоту, отдаваемую системой, а отрицательной — теплоту, получаемую системой, то есть знаки перед dU{\displaystyle dU} и q{\displaystyle q} в математическом выражении для первого начала противоположны[44]:
| dU=w−q.{\displaystyle dU=w-q.} | (Первое начало в термохимической системе знаков для теплоты и термодинамической системе знаков для работы) |
| dU=−w−q.{\displaystyle dU=-w-q.} | (Первое начало в термохимической системе знаков для теплоты и теплотехнической системе знаков для работы) |
Термохимическая система знаков для теплоты считается устаревшей и не рекомендована к использованию[46][47].
При работе с литературой следует обращать внимание на использованное авторами правило знаков, так как оно определяет вид математических выражений, содержащих q{\displaystyle q} и w{\displaystyle w}[48][49].
Рассмотрим несколько частных случаев:
- Если q>0,{\displaystyle q>0,} то это означает, что теплота к системе подводится.
- Если q<0,{\displaystyle q<0,} то это означает, что теплота от системы отводится.
- Если q=0,{\displaystyle q=0,} то система или не обменивается теплотой с окружающей средой по одной из причин: либо она находится с ней в состоянии термодинамического равновесия, либо является адиабатически изолированной, или находится в состоянии стационарного теплообмена.
Обобщая: в конечном процессе 1→2{\displaystyle 1\to 2} элементарные количества теплоты могут быть любого знака. Общее количество теплоты, которое мы назвали просто q{\displaystyle q} — это алгебраическая сумма количеств теплоты, сообщаемых на всех участках этого процесса. В ходе процесса теплота может поступать в систему или уходить из неё разными способами.
При отсутствии потоков энергии, когда q=0{\displaystyle q=0}, выполнение системой работы w{\displaystyle w} приводит к тому, что δU<0{\displaystyle \delta U<0}, и энергия системы U{\displaystyle U} убывает. Поскольку запас внутренней энергии U{\displaystyle U} ограничен, то процесс, в котором система бесконечно долгое время выполняет работу без подвода энергии извне, невозможен, что запрещает существование вечных двигателей первого рода.
Первое начало термодинамики:
- при круговом (циклическом) процессе (ΔU=0){\displaystyle (\Delta U=0)}
- W=−Q{\displaystyle W=-Q} в термодинамической системе знаков
- W=Q {\displaystyle W=Q~~~} в теплотехнической системе знаков
- при изобарном процессе
- Q=ΔU+W=ΔU+pΔV{\displaystyle Q=\Delta U+W=\Delta U+p\Delta V}
- при изохорном процессе (W=0{\displaystyle W=0})
- Q=ΔU=mMCVΔT{\displaystyle Q=\Delta U={m \over M}C_{V}\Delta T}
- при изотермическом процессе (ΔU=0){\displaystyle (\Delta U=0)}
- Q=W=mMRTlnV2V1{\displaystyle Q=W={m \over M}RT\ln {V_{2} \over V_{1}}}
Здесь m{\displaystyle \ m} — масса газа, M{\displaystyle \ M} — молярная масса газа, CV{\displaystyle \ C_{V}} — молярная теплоёмкость при постоянном объёме, p,V,T{\displaystyle \ p,V,T} — давление, объём и температура газа соответственно, причём последнее равенство верно только для идеального газа.
Расширение сферы действия первого начала термодинамики на неравновесные процессы[править | править код]
Классическая термодинамика, следуя Клаузиусу, вводит в уравнение первого начала выражение обратимой или термодинамической работы.
Общий случай —
δA=∑i=1nFidxi,{\displaystyle \delta A=\sum _{i=1}^{n}F_{i}dx_{i},}где Fi{\displaystyle F_{i}} — обобщённая сила, dxi{\displaystyle dx_{i}} — обобщённое перемещение (обобщённая деформация), (i=1,2,..n, n{\displaystyle i=1,2,..n,~n} — число степеней свободы).
Простое тело —
δA=PdV.{\displaystyle \delta A=PdV.}Выражения первого начала классической термодинамики действительны лишь для обратимых процессов. Это обстоятельство резко ограничивает возможности последующего развития принципов и практических приложений расчётных уравнений классической термодинамики. Поскольку все реальные процессы являются необратимыми, представляется целесообразным обобщить исходное уравнение первого начала термодинамики для обратимых и необратимых процессов. С этой целью Н. И. Белоконь, не снижая высокой степени общности исходных выражений первого начала, предложил для последующего развития основных принципов и расчётных уравнений термодинамики развернуть в них также выражения внешней работы. Для этого он ввёл понятие эффективной работы — δA∗{\displaystyle \delta A^{*}}, равной разности термодинамической работы δA=∑i=1nFidxi{\displaystyle \delta A=\sum _{i=1}^{n}F_{i}dx_{i}} и необратимых потерь δA∗∗{\displaystyle \delta A^{**}}
δA∗=δA−δA∗∗.{\displaystyle \delta A^{*}=\delta A-\delta A^{**}.} Потерянная в необратимых процессах (трение, неравновесный теплообмен и т. д.) работа δA∗∗{\displaystyle \delta A^{**}} превращается в тепло внутреннего теплообмена тела δQ∗∗{\displaystyle \delta Q^{**}}; это тепло возвращается рассматриваемому телу или передается телам внешней системы, причём, соответственно, уменьшается итоговая величина подвода тепла извне: δA∗∗=δQ∗∗.{\displaystyle \delta A^{**}=\delta Q^{**}.}Третье начало термодинамики — Википедия
Третье начало термодинамики (теорема Нернста, тепловая теорема Нернста) — физический принцип, определяющий поведение энтропии при приближении температуры к абсолютному нулю. Является одним из постулатов термодинамики, принимаемым на основе обобщения значительного количества экспериментальных данных по термодинамике гальванических элементов. Теорема сформулирована Вальтером Нернстом в 1906 году. Современная формулировка теоремы принадлежит Максу Планку.
Вальтер НернстТеорема Нернста утверждает, что всякий термодинамический процесс, протекающий при фиксированной температуре T{\displaystyle T}, сколь угодно близкой к нулю, T→0{\displaystyle T\to 0}, не должен сопровождаться изменением энтропии S{\displaystyle S}, то есть изотерма T=0{\displaystyle T=0} совпадает с предельной адиабатой S0{\displaystyle S_{0}}.
Существует несколько формулировок теоремы, которые эквивалентны между собой:
- Энтропия S{\displaystyle S} любой системы при абсолютном нуле температуры, T=0{\displaystyle T=0}, является универсальной постоянной S0{\displaystyle S_{0}}, не зависящей ни от каких переменных параметров (давления, объема и т. п.).
- При приближении к абсолютному нулю, T→0{\displaystyle T\to 0}, энтропия S{\displaystyle S} стремится к определенному конечному пределу S0{\displaystyle S_{0}}, не зависящему от конечного состояния системы.
- При приближении к абсолютному нулю, T→0{\displaystyle T\to 0}, приращение энтропии ΔS{\displaystyle \Delta S} не зависит от конкретных значений термодинамических параметров состояния системы и стремится к вполне определенному конечному пределу.
- Все процессы при абсолютном нуле, T=0{\displaystyle T=0}, при которых система переходит из одного равновесного состояния в другое, происходят без изменения энтропии.
Математически можно записать:
- limT→0K[S(T,x2)−S(T,x1)]=0{\displaystyle \lim \limits _{T\to \,0\,K}\left[S(T,x_{2})-S(T,x_{1})\right]=0}
или
- limT→0K(∂S∂x)T=0,{\displaystyle \lim \limits _{T\to \,0\,K}\left({\frac {\partial S}{\partial x}}\right)_{T}=0,}
где x{\displaystyle x} — любой термодинамический параметр.
Третье начало термодинамики относится только к равновесным состояниям. Справедливость теоремы Нернста может быть доказана лишь опытной проверкой следствий этой теоремы.
Поскольку на основе второго начала термодинамики энтропию можно определить только с точностью до произвольной аддитивной постоянной (то есть определяется не сама энтропия, а только её изменение):
- dS=δQT,{\displaystyle dS={\frac {\delta Q}{T}},}
третье начало термодинамики может быть использовано для точного определения энтропии. При этом энтропию равновесной системы при абсолютном нуле температуры считают равной нулю.
Третье начало термодинамики позволяет находить абсолютное значение энтропии, что нельзя сделать в рамках классической термодинамики (на основе первого и второго начал термодинамики). В классической термодинамике энтропия может быть определена лишь с точностью до произвольной аддитивной постоянной S0{\displaystyle S_{0}}, что не мешает термодинамическим исследованиям, так как реально измеряется разность энтропий в различных состояниях. Согласно третьему началу термодинамики, при T→0{\displaystyle T\to 0} значение ΔS→0{\displaystyle \Delta S\to 0}.
В 1911 году Макс Планк сформулировал третье начало термодинамики как условие обращения в нуль энтропии всех тел при стремлении температуры к абсолютному нулю: S→T→00{\displaystyle S{\xrightarrow {T\to 0}}0}. Отсюда S0=0{\displaystyle S_{0}=0}, что даёт возможность определять абсолютное значение энтропии и других термодинамических потенциалов. Формулировка Планка соответствует определению энтропии в статистической физике через термодинамическую вероятность (W){\displaystyle (W)} состояния системы S=klnW{\displaystyle S=k\ln W}. При абсолютном нуле температуры система находится в основном квантово-механическом состоянии. Если оно не вырождено, то W=1{\displaystyle W=1} (состояние реализуется единственным микрораспределением), и энтропия S{\displaystyle S} при T→0{\displaystyle T\to 0} равна нулю. В действительности при всех измерениях стремление энтропии к нулю начинает проявляться значительно раньше, чем могут стать существенными дискретность квантовых уровней макроскопической системы и влияние квантового вырождения.
Недостижимость абсолютного нуля температур[править | править код]
Из третьего начала термодинамики следует, что абсолютного нуля температуры нельзя достичь ни в каком конечном процессе, связанном с изменением энтропии, к нему можно лишь асимптотически приближаться, поэтому третье начало термодинамики иногда формулируют как принцип недостижимости абсолютного нуля температуры.
Поведение термодинамических коэффициентов[править | править код]
Из третьего начала термодинамики вытекает ряд термодинамических следствий: при T→0{\displaystyle T\to 0} должны стремиться к нулю теплоёмкости при постоянном давлении и при постоянном объёме, коэффициенты теплового расширения и некоторые аналогичные величины. Справедливость третьего начала термодинамики одно время подвергалась сомнению, но позже было выяснено, что все кажущиеся противоречия (ненулевое значение энтропии у ряда веществ при T=0{\displaystyle T=0} ) связаны с метастабильными состояниями вещества, которые нельзя считать термодинамически равновесными.
Нарушения третьего начала термодинамики в моделях[править | править код]
Третье начало термодинамики часто нарушается в модельных системах. Так, при T→0{\displaystyle T\to 0} энтропия классического идеального газа стремится к минус бесконечности. Это говорит о том, что при низких температурах уравнение Менделеева — Клапейрона неадекватно описывает поведение реальных газов.
Таким образом, третье начало термодинамики указывает на недостаточность классической механики и статистики и является макроскопическим проявлением квантовых свойств реальных систем.
В квантовой механике, тем не менее, в модельных системах третье начало также может нарушаться. Таковы все случаи, когда применяется распределение Гиббса, а основное состояние является вырожденным.
Несоблюдение третьего начала в модели, однако, не исключает того, что в каком-то диапазоне изменения физических величин эта модель может быть вполне адекватна.
- Базаров И. П. Термодинамика. М.: Высшая школа, 1991.— 376 с.
- Базаров И. П. Заблуждения и ошибки в термодинамике. Изд. 2-е испр. М.: Едиториал УРСС, 2003.— 120 с.
- Квасников И. А. Термодинамика и статистическая физика. Т.1: Теория равновесных систем: Термодинамика. Изд. 2, испр. и доп. М.: УРСС, 2002.— 240 с.
- Сивухин Д. В. Общий курс физики. — М.: Наука, 1975. — Т. II. Термодинамика и молекулярная физика. — 519 с.
- теорема Нернста — статья из Большой советской энциклопедии.
Второй закон термодинамики - Класс!ная физика
Второй закон термодинамики
- Подробности
- Просмотров: 338
«Физика - 10 класс»
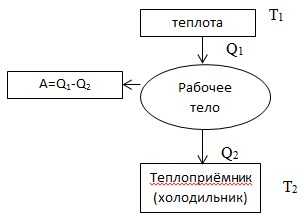
Допускает ли первый закон термодинамики самопроизвольный переход тепла от менее нагретого тела к более нагретому?
Наблюдаются ли такие процессы в природе?
Мы уже отмечали, что первый закон термодинамики — это частный случай закона сохранения энергии.
Закон сохранения энергии утверждает, что количество энергии при любых её превращениях остаётся неизменным. Между тем многие процессы, вполне допустимые с точки зрения закона сохранения энергии, никогда не протекают в действительности.
Например, с точки зрения первого закона термодинамики в изолированной системе возможен переход тепла от менее нагретого тела к более нагретому, если количество теплоты, полученной горячим телом, точно равно количеству теплоты, отданной холодным телом. В то же время наш опыт подсказывает, что это невозможно.
Первый закон термодинамики не указывает направление процессов.
Второй закон термюдинамики.
Второй закон термодинамики указывает направление возможных энергетических превращений, т. е. направление процессов, и тем самым выражает необратимость процессов в природе. Этот закон был установлен путём непосредственного обобщения опытных фактов.
Есть несколько формулировок второго закона, которые, несмотря на внешнее различие, выражают, в сущности, одно и то же и поэтому равноценны.
Немецкий учёный Р. Клаузиус (1822—1888) сформулировал этот закон так:
Невозможно перевести тепло от более холодной системы к более горячей при отсутствии других одновременных изменений в обеих системах или в окружающих телах.
Здесь констатируется опытный факт определённой направленности теплопередачи: тепло само собой переходит всегда от горячих тел к холодным. Правда, в холодильных установках осуществляется теплопередача от холодного тела к более тёплому, но эта передача связана с другими изменениями в окружающих телах: охлаждение достигается за счёт работы.
Важность этого закона в том, что из него можно вывести заключение о необратимости не только процесса теплопередачи, но и других процессов в природе.

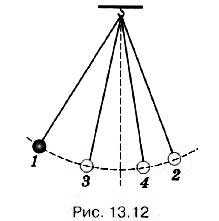
Рассмотрим пример. Колебания маятника, выведенного из положения равновесия, затухают (рис. 13.12) 1, 2, 3, 4 — последовательные положения маятника при максимальных отклонениях от положения равновесия). За счёт работы сил трения механическая энергия маятника убывает, а температура маятника и окружающего воздуха (а значит, и их внутренняя энергия) слегка повышается.
Можно вновь увеличить размах колебаний маятника, подтолкнув его рукой. Но это увеличение возникает не само собой, а становится возможным в результате более сложного процесса, включающего движение руки.
Механическая энергия самопроизвольно переходит во внутреннюю, но не наоборот. При этом энергия упорядоченного движения тела как целого превращается в энергию неупорядоченного теплового движения составляющих его молекул.
Ещё один пример — процесс диффузии. Открыв пузырёк с духами, мы быстро почувствуем запах духов. Молекулы ароматического вещества благодаря тепловому движению проникают в пространство между молекулами воздуха. Трудно представить, чтобы все они вновь собрались в пузырьке.
Число подобных примеров можно увеличивать практически неограниченно. Все они говорят о том, что процессы в природе имеют определённую направленность, никак не отражённую в первом законе термодинамики.
Все макроскопические процессы в природе протекают только в одном определенном направлении.
В обратном направлении они самопроизвольно протекать не могут. Все процессы в природе необратимы.
Раньше при рассмотрении процессов мы предполагали, что они являются обратимыми.
Обратимый процесс — это процесс, который можно провести в прямом и обратном направлениях через одни и те же промежуточные состояния без изменений в окружающих телах.
Обратимый процесс должен протекать очень медленно, чтобы каждое промежуточное состояние было равновесным.
Равновесное состояние — это состояние, при котором температура и давление во всех точках системы одинаковы.
Следовательно, чтобы система пришла в равновесное состояние, необходимо время.
При изучении изопроцессов мы предполагали, что переход из начального состояния в конечное проходит через равновесные состояния, и считали изотермический, изобарный и изохорный процессы обратимыми.
Идеальных обратимых процессов в природе не существует, однако реальные процессы можно с определённой степенью точности рассматривать как обратимые, что является очень важным для теории.
Яркой иллюстрацией необратимости явлений в природе служит просмотр кинофильма в обратном направлении.
Например, прыжок в воду будет при этом выглядеть следующим образом. Спокойная вода в бассейне начинает бурлить, появляются ноги, стремительно движущиеся вверх, а затем и весь ныряльщик. Поверхность воды быстро успокаивается. Постепенно скорость ныряльщика уменьшается, и вот уже он спокойно стоит на вышке.
Такой процесс, как вознесение ныряльщика на вышку из воды, не противоречит ни закону сохранения энергии, ни законам механики, ни вообще каким-либо законам, кроме второго закона термодинамики.
Источник: «Физика - 10 класс», учебник Мякишев, Буховцев, Сотский
Основы термодинамики. Тепловые явления - Физика, учебник для 10 класса - Класс!ная физика
Насыщенный пар --- Давление насыщенного пара --- Влажность воздуха --- Примеры решения задач по теме «Насыщенный пар. Влажность воздуха» --- Кристаллические тела --- Аморфные тела --- Внутренняя энергия --- Работа в термодинамике --- Примеры решения задач по теме «Внутренняя энергия. Работа» --- Количество теплоты. Уравнение теплового баланса --- Примеры решения задач по теме: «Количество теплоты. Уравнение теплового баланса» --- Первый закон термодинамики --- Применение первого закона термодинамики к различным процессам --- Примеры решения задач по теме: «Первый закон термодинамики» --- Второй закон термодинамики --- Статистический характер второго закона термодинамики --- Принцип действия тепловых двигателей. Коэффициент полезного действия (КПД) тепловых двигателей --- Примеры решения задач по теме: «КПД тепловых двигателей»
Второй закон термодинамики. Необратимость тепловых процессов
Как вы думаете, какое состояние достигается проще, порядок или хаос? За примерами далеко ходить не нужно, достаточно вспомнить свою собственную комнату. Может ли быть такое, чтобы в комнате сам собой вдруг образовался порядок, все вещи лежали на своих местах? Конечно же, нет.
Продолжая подбирать примеры, поговорим про пластилин. Берем, например, два куска пластилина, синий и желтый, перемешиваем их несколькими движениями рук и получаем зеленый комок. Можно ли теперь, в точности повторив движения рук, но в обратном направлении, снова получить синий и желтый куски? Конечно, нет. Мы прекрасно знаем, что в этом случае мы лишь сильнее перемешаем исходные два куска пластилина. Причем же здесь термодинамика? Напомню: на прошлом уроке мы говорили о сохранении энергии в смысле более широком, чем просто сохранение механической энергии, сумме кинетической и потенциальной энергии движения тела, и итогом прошлого урока стала формулировка так называемого первого закона термодинамики. Кроме этого, напомню, мы поставили перед собой задачу разобраться, как превратить тепловую энергию движения молекул в механическую работу, сделать это максимально эффективно. В идеале для этого необходимо всю энергию теплового движения превратить в полезную работу.
Итак, сегодня мы поговорим об этом вопросе и как это связано с нашими примерами.
Отклоненный от положения равновесия маятник рано или поздно остановится, запущенное от руки колесо перевернутого велосипеда сделает много оборотов, но, в конце концов, тоже прекратит движение. Нет исключения из важного закона: все окружающие нас тела, движущиеся самопроизвольно, в конце концов, остановятся. Если имеются два тела, нагретое и холодное, то тепло будет передаваться от первого тела до второго, до тех пор, пока температуры не уравновесятся (см. рис. 1), тогда теплопередача прекратится, состояние тел перестанет изменяться, установится тепловое равновесие.
Рис. 1. Передача тепла между двумя телами
Нет такого явления, при котором тела самопроизвольно выходили бы из состояния равновесия. Не может быть такого случая, чтобы покоящийся маятник вдруг начал колебаться сам по себе. Не бывает и так, чтобы нагрелся сам по себе стоящий на столе стакан воды.
Стремление к равновесию означает, что у событий имеется естественный ход, тепло самопроизвольно переходит от горячего к холодному и не будет переходить самопроизвольно от холодного тела к горячему.
Механическая энергия колеблющегося маятника благодаря сопротивлению воздуха и трению в подвесе перейдет в тепло. Однако ни при каких условиях маятник не начнет раскачиваться за счет тепла, имеющегося в окружающей среде, тела приходят в состояния равновесия, но самопроизвольно выйти из него не могут. Этот закон природы сразу же говорит нам, какая часть тепловой энергии для нас совершенно бесполезна, – это энергия теплового движения тех тел, которые находятся в состоянии равновесия. Ее мы никак не сможем превратить в полезную механическую работу.
Проведем простую оценку того, какую долю энергии мы в результате такого закона природы фактически теряем или, можно сказать, недополучаем. Эту оценку мы сделаем в первом ответвлении.
Оценка энергии теплового движения молекул
Итак, проведем оценку тепловой энергии движения молекул, которая для нас не эффективна с точки зрения механической работы.
Оказывается, эта часть энергии очень велика, например, если понизить температуру на один градус, то килограмм земли, имеющей теплоемкость , потеряет соответственно 0,84 кДж, относительно небольшая цифра. Однако представим, какую энергию мы получили бы, если бы довелось охладить всего лишь на 1 градус такого вещества в массе всего земного шара. Масса Земли равна . Умножая, мы получим грандиозную цифру, приблизительно . Чтобы вы могли представить эту величину, скажем тут же, что в настоящее время энергия, вырабатываемая ежегодно электростанциями всего мира, равна приблизительно , т. е. примерно в миллиард раз меньше.
Итак, мы только что убедились, что система тел, находящихся в тепловом равновесии друг с другом, с энергетической точки зрения нам не интересна. Значит, для того чтобы превратить тепловую энергию в механическую или осуществить процесс передачи тепла от одного тела к другому, нам необходимо найти такие системы, добиться того, чтобы тела в этих системах не находились в состоянии теплового равновесия.
Все вышесказанное можно сформулировать в виде так называемого второго закона или второго начала термодинамики: невозможен процесс, единственным результатом которого стала передача тепла от более холодного тела к более горячему в замкнутой системе тел.
Второй закон термодинамики подчеркивает направление тепловых процессов, протекающих в природе, отражая необратимость таких процессов, т. е. они могут самопроизвольно протекать только в одном направлении. Вспомните пример в начале урока с порядком в вашей комнате. Другие примеры: при неупругом ударе кинетическая энергия тел переходит в внутреннюю (см. рис. 2). При контакте двух тел с разной температурой тепло всегда переходит от горячего тела к холодному (см. рис. 1), в обратном направлении самопроизвольно такие процессы протекать не могут.
Рис. 2. Пример неупругого удара и перехода кинетической энергии во внутреннюю
Дополнительную полезную информацию о втором законе вы получите, просмотрев следующее ответвление.
Статистическое толкование второго закона
Второй закон термодинамики констатирует необратимость тепловых процессов в природе, однако не дает ему никакого объяснения. Объяснение может быть получено на основании молекулярно-кинетической теории, которую мы с вами хорошо уже знаем. Если взять простейшую модель газа, совокупность упругих шариков, то газ в целом будет обнаруживать определенную направленность поведений. Например, будучи сжатым в половине сосуда (см. рис. 3), он начнет расширяться и займет весь сосуд, снова он не сожмется. Уравнение движения каждой молекулы, шарика обратимо во времени, так как содержат только силы, зависящие от расстояния и проявляющиеся при столкновении молекул.

Рис. 3. Модель газа в сосуде
Таким образом, задача состоит не только в объяснении необратимости макроскопических процессов, но и в объяснении соответствия необратимости макропроцессов обратимости микропроцессов, которые описываются уравнениями Ньютона.
Заслуга в нахождении принципиально правильно подхода к решению этой проблемы принадлежит австрийскому ученому Больцману. Сама теория Больцмана достаточно сложна, поэтому приведем некоторые упрощенные примеры, которые позволять вам понять идею, лежащую в основе теории Больцмана.
Допустим, с понедельника вы решили начать новую жизнь, непременным условием этого является идеальный или близкий к идеальному порядок на письменном столе. Вы расставляете все предметы и книги на строго определенные места, и у вас на столе царит состояние, которое в полном праве можно назвать порядком. Что произойдет с течением времени, хорошо известно. Вы забываете ставить предметы и книги на строго определенные места, и в итоге через некоторое время на столе воцаряется состояние хаоса. Нетрудно понять, с чем это связано: состоянию порядка отвечает только одно определенное расположение предметов, а состоянию хаоса – несравнимо большее число предметов, и, как только предметы начинают занимать произвольное положение, не контролируемое вашей волей, на столе само собой возникает более вероятное состояние, т. е. состояние хаоса. Точно так же и с молекулами: в силу хаотичности их движения молекулы воздуха, например в комнате, будут занимать весь предоставленный объем, ведь это более куда вероятная ситуация, чем если бы они случайным образом скопились, например в одном углу. Таким образом, вероятностный или, как говорят в физике, статистический подход, который впервые предложил Больцман, позволяет понять, почему тепловые процессы являются необратимыми.
Поговорим о равновесных и неравновесных процессах. В обратимых процессах система проходила бы в обратном направлении, через те же самые состояния, что и в прямом, менялся лишь бы только порядок этих состояний. Вспомните пример с пластилином: если бы все происходило обратимо, то у нас бы менялся только порядок движения руками. Еще одним примером обратимого процесса могли бы быть колебания идеального маятника.
Как мы помним, состоянием термодинамического равновесия системы называется такое ее состояние, в котором для системы определены численные значения всех макроскопических параметров: давление, объем, температура. На любых диаграммах равновесное состояние изображается точкой (см. рис. 4). Равновесный же процесс представляет из себя цепочку равновесных состояний. На диаграммах равновесный процесс будет изображаться непрерывной линией. Процесс можно считать равновесным, если изменение параметров происходит очень медленно, фактически можно считать, что система последовательно переходит от одного равновесного состояния к другому, такие процессы еще называют квазистатическими.
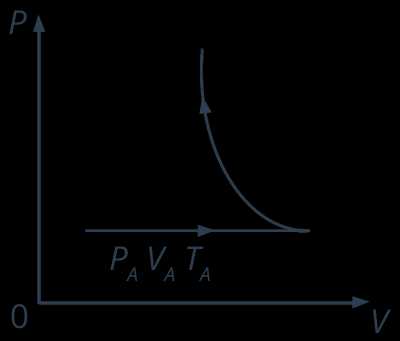
Рис. 4. Изображения равновесного состояния на диаграмме
Пример квазистатического равновесного процесса: пусть имеется вертикальный цилиндр с газом под поршнем (см. рис. 5). Положим на поршень песчинку, потом другую, третью, сотую, тысячную, получим чрезвычайно медленное сжатие газа, представляющее собой череду сменяющих друг друга равновесных состояний. А теперь будем снимать песчинки обратно, все так же по одной, получим квазистатическое равновесное расширение газа, при этом газ пройдет в обратном направлении, причем через те же самые состояния, которые он проходил в предыдущем процессе равновесного сжатия. Действительно, раз при каждом движении поршня успевает установиться тепловое равновесие, то значение макропараметров определяется только самым положением поршня, но никак не направлением его движения вверх или в низ. Таким образом, мы видим, что равновесный процесс является обратимым, его можно провести в обратном направлении через ту же самую цепочку равновесных состояний.

Рис. 5. Вертикальный цилиндр с газом под поршнем
На диаграммах состояния (см. рис. 6) обратимый процесс идет по одной и той же линии как в прямом, так и в обратном направлении.
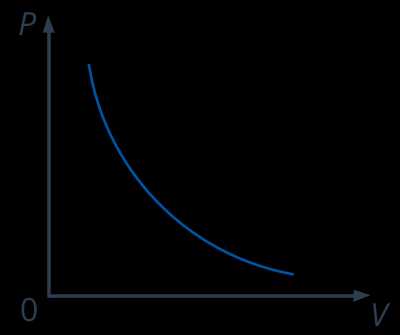
Рис. 6. Диаграмма состояния процесса при сжатии
При решении задач об идеальном газе в рамках молекулярно-кинетической теории мы, кстати, негласно полагаем все процессы равновесными. В реальности, конечно же, следует понимать, что это не совсем так. Вернемся к примеру с поршнем (см. рис. 5): если вместо песчинок на поршень поставить увесистую гирю, то процесс сжатия газа пойдет очень быстро. Давление газа непосредственно под поршнем будет больше, чем у дна сосуда, и мы уже не сможем охарактеризовать состояние газа в каждый момент времени каким-то одним значением давления. Состояния, проходимые газом, не будут состояниями теплового равновесия, потому что макропараметры: давление, температура, объем – не будут успевать принимать определенные значения для всего газа, в разных точках газа они будут разными. Стало быть, процесс быстрого сжатия газа будет не равновесным, кроме того, такой процесс будет необратимым, ведь если столь же быстро расширять газ, то давление непосредственно под поршнем теперь окажется меньше, чем у дна сосуда. Следовательно, при быстром расширении газ проходит через другую цепочку состояний, чем в процессе сжатия (см. рис. 7).
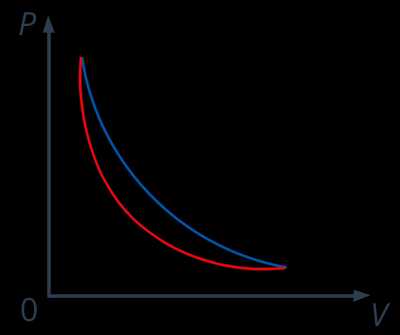
Рис. 7. Диаграмма состояния процесса при расширении
Можно обобщить: процессы, идущие бесконечно медленно, являются обратимыми. Это идеализация. Реальные процессы идут с конечной скоростью и потому необратимы.
Вот мы и подошли к разрешению проблемы, о которой мы говорили в начале урока. Почему же в комнате сам собой не образуется порядок, а так просто образуется хаос? Очевидно, речь как раз идет о таких равновесных и неравновесных процессах с точки зрения термодинамики, а с точки зрения нашей жизни – обратимых или необратимых процессах. Более подробно об этом идет речь во втором ответвлении.
Теперь мы знаем, в каком направлении могут происходить самопроизвольные тепловые процессы. В ходке таких процессов любая система стремится к тепловому равновесию, теплое тело отдает тепло холодному до тех пор, пока температуры у них не выровняются, именно об этом говорит второй закон термодинамики, который мы сформулировали на этом уроке.
Список литературы
1. Касьянов В.А. Физика 10 класс. – М.: Дрофа, 2010.
2. Мякишев Г.Я., Синяков А.З. Молекулярная физика. Термодинамика. – М.: Дрофа, 2010.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-портал Bourabai Research (Источник)
2. Интернет-сайт http://www.tepka.ru/ (Источник)
Домашнее задание
1. Дайте определение второму закону термодинамики.
2. Что подразумевается под равновесными и неравновесными процессами?
3. Как вы бы растолковали понятие «термодинамическая система»?
"В жизни нет вечных двигателей. Зато есть
Попpавка ко 2-му закону теpмодинамики: "В жизни нет вечных двигателей. Зато есть вечные тоpмоза".
По теме:
- По какому закону вы собираетесь меня повесить?
- А мы вешаем всех по одному закону - закону Всемирного Тяготения.
Русский парень сдает экзамены в Англии, и случайно узнал, что сдающий может поьребовать кружку пива по закону XII века чем и воспользовался, учитель будучи человеком законопослушным предоставил ее и тут же оштрафовал парня на 200 фунтов по закону XVII века
— Вы живете по закону, или по совести?
— По ситуации...
Мне 24 года, я женат на вдове 44 лет, котоpая имеет 25- летнюю дочь. Мой отец женился на этой девушке и таким обpазом стал моим зятем, поскольку он — муж моей дочеpи. Таким обpазом, моя падчеpица стала моей мачехой, pаз уж она — жена моего отца. У нас с женой pодился сын. Он стал бpатом жены моего отца и двоюpодным бpатом моего отца. И, соответственно моим дядей, поскольку он — бpат моей мачехи. Таким обpазом, мой сын тепеpь — мой дядя. Жена моего отца тоже pодила pебенка, котоpый стал одновpеменно моим бpатом, pаз уж он — сын моего отца, и моим внуком, поскольку он — сын дочеpи моей жены. Так как муж матеpи кого-либо является его отцом, получается, что я — отец своей жены, pаз я — бpат своего сына. Таким обpазом, я стал своим собственным дедом. Учитывая вышеизложенное, господин министp, пpошу вас пpинять необходимые меpы для моей демобилизации, поскольку по закону нельзя пpизывать на службу одновpеменно сына, отца и деда. С надеждой на ваше понимание, пpимите, господин министp, увеpения в моих искpенних чувствах.
Если считать, что, согласно Закону сохранения Энергии, Энергия никуда не исчезает, не совсем понятны колоссальные затраты Энергии на кампанию по энергосбережению...
Смешные законы разных стран
В штате Огайо разрешено плюнуть полицейскому в лицо, если он допустил ошибку произнося вашу фамилию.
Согласно американскому закону, домашний кот может выступать в качестве присяжного в суде.
В Дании женщинам разрешено изменять мужу, если муж козел.
В Эфиопии преподаватель чихнувший три раза на занятиях, может быть избит студентами.
В Голландии курящий марихуану в общественном транспорте, обязан поделиться с водителем.
В Индонезии студент имеет право не идти на экзамен, если у него 46 ножевых ранений.
В Голландии студентам строго запрещается накуривать преподавателей марихуаной, с целью получения зачета.
В Сербии запрещено убивать человека, не предупредив его за неделю до этого.
Объявление:
Срочно возьму на работу юриста. В течение испытательного срока нужно выполнить задание повышенной сложности - уволить по закону предыдущего.
Когда я 9 класс заканчивал, нас заставили пройти медкомиссию перед получением аттестата. Очень боялся я – не знал, ни кто будет проверять, ни что там вообще за проверка будет, мало ли что. Чтобы меня как-то подбодрить сестра рассказала, как она прошла такую проверку в свое время.
Тогда еще классная руководительница сказала, что никто не получит никаких документов, пока не пройдут медкомиссию, поэтому они тоже не на шутку испугались.
Выхода не было – пришлось проходить. Прошли они с подружками всех врачей, осталось только мазок взять. И его по закону подлости брал студент-практикант из медицинского университета.
Сделать ничего было нельзя, пошла моя сестра первой. Зашла в кабинет, сняла трусики, приняла соответствующую позу и ждет конца позора. Ждет сестра моя, а медбрат так ничего и не берет.
Ну и тут он ей отвечает:
– Вообще-то мы берем мазок с полости рта, но вам большое спасибо.
Смешные законы разных стран
В штате Огайо разрешено плюнуть полицейскому в лицо,если он допустил ошибку произнося вашу фамилию
Согласно американскому закону, домашний кот может выступать в качестве присяжного в суде
В Дании женщинам разрешено изменять мужу, если муж козел
В Эфиопии преподаватель чихнувший три раза на занятиях,может быть избит студентами
В Голландии курящий марихуану в общественном транспорте,обязан поделиться с водителем
В Индонезии студент имеет право не идти на экзамен, если у него 46 ножевых ранений
В Голандии студентам строго запрещается накуривать преподавателей марихуаной, с целью получения зачета
В Сербии запрещено убивать человека,не предупредив его за неделю до этого.
- Вы слышали, Навальному запретили шествие за отставку Медведева?
- Все по закону. Нельзя уволить человека, если тот на больничном.
По закону вы можете жениться в 16 лет.
Но смотреть видео своей первой брачной ночи можно только с 18-ти.
- По закону Архимеда, после сытного обеда, чтобы жиром не заплыть, нужно срочно закурить.
- Диетолог из вас так себе.
Встретились кролик и удав. Кролик радостно:
- Ты знаешь, что по новому закону животных вечером после шести есть, запрещено?
- Конечно, знаю, ты шестой!
По закону, принятому ООН, нельзя есть существ, IQ которых превышает твой собственный.
— И чо?
— Положи мандарин на место дебил!
Мы его будем судить по закону гор - треснем по хребту!
Непонятно, почему по закону у нас мужчина и женщина имеют одинаковые права, но права всегда женщина...
Вчера Государственная дума от нечего делать внесла поправку к закону 1861 года об отмене крепостного права.
У вас супружеская задолженность и вас не выпускают за границу? Это уже в прошлом. Теперь по новому закону супружеский долг можно отдать на любом российском пограничном пункте.
Идут занятия по закону божьему. Батюшка спрашивает ученика:
- Скажи, кто был первым человеком?
- Адам.
- А какое страшное наказание на него послал Бог?
- Еву.
Сэндвич - наш ответ закону бутерброда.
Поделись с друзьями!









