-
Свежие записи
Рубрики
- Анекдоты (512)
- Афоризмы (12)
- Всякое-разное (15)
- Демотиваторы (11)
- Прикольное и смешное видео (20)
- Прикольные истории (8)
- Прикольные картинки (47)
- Прикольные стишки (44)
- Прикольные фотки (18)
- Просто шутки (71)
Приглашаю присоединиться ко мне в следующих сервисах:
Другие функции:

Анекдот про правило лопиталя
Правило Лопиталя — Википедия
Материал из Википедии — свободной энциклопедии
Теорема Лопита́ля (также правило Бернулли — Лопиталя[1]) — метод нахождения пределов функций, раскрывающий неопределённости вида 0/0{\displaystyle 0/0} и ∞/∞{\displaystyle \infty /\infty }. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Теорема Лопиталя:
Если: f(x),g(x){\displaystyle f(x),\,g(x)} — действительнозначные функции, дифференцируемые в проколотой окрестности U{\displaystyle U} точки a{\displaystyle a}, где a{\displaystyle a} — действительное число или один из символов +∞,−∞,∞{\displaystyle +\infty ,-\infty ,\infty }, причём
- limx→af(x)=limx→ag(x)=0{\displaystyle \lim _{x\to a}{f(x)}=\lim _{x\to a}{g(x)}=0} или ∞{\displaystyle \infty };
- g′(x)≠0{\displaystyle g'(x)\neq 0} в U{\displaystyle U};
- существует limx→af′(x)g′(x){\displaystyle \lim \limits _{x\to a}{\frac {f'(x)}{g'(x)}}};
тогда существует limx→af(x)g(x)=limx→af′(x)g′(x){\displaystyle \lim \limits _{x\to a}{\frac {f(x)}{g(x)}}=\lim \limits _{x\to a}{\frac {f'(x)}{g'(x)}}}.
Пределы также могут быть односторонними.
Способ раскрытия такого рода неопределённостей был опубликован в учебнике «Analyse des Infiniment Petits» 1696 года за авторством Гийома Лопиталя. Метод был сообщён Лопиталю в письме его первооткрывателем Иоганном Бернулли.[2]
- limx→0x2+5x3x=limx→02x+53=53{\displaystyle \lim _{x\to 0}{\frac {x^{2}+5x}{3x}}=\lim _{x\to 0}{\frac {2x+5}{3}}={\frac {5}{3}}}
Простое, но полезное следствие правила Лопиталя — признак дифференцируемости функций, состоит в следующем:
Пусть функция f(x){\displaystyle f(x)} дифференцируема в проколотой окрестности точки a{\displaystyle a}, а в самой этой точке она непрерывна и имеет предел производной limx→af′(x)=A{\displaystyle \lim _{x\to a}f'(x)=A}. Тогда функция f(x){\displaystyle f(x)} дифференцируема и в самой точке a{\displaystyle a}, и f′(a)=A{\displaystyle f'(a)=A} (то есть, производная f′(x){\displaystyle f'(x)} непрерывна в точке a{\displaystyle a}).
Для доказательства достаточно применить правило Лопиталя к отношению f(x)−f(a)x−a{\displaystyle {\frac {f(x)-f(a)}{x-a}}}.
Аналогом правила Лопиталя для последовательностей вещественных чисел является Теорема Штольца.
Правило Лопиталя: теория и примеры решений
Производная от функции недалеко падает, а в случае правил Лопиталя она падает точно туда же, куда падает исходная функция. Это обстоятельство помогает в раскрытии неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей, возникающих при вычислении предела отношения двух бесконечно малых или бесконечно больших функций. Вычисление значительно упрощается с помощью этого правила (на самом деле двух правил и замечаний к ним):
.
Как показывает формула выше, при вычислении предела отношений двух бесконечно малых или бесконечно больших функций предел отношения двух функций можно заменить пределом отношения их производных и, таким образом, получить определённный результат.
Перейдём к более точным формулировкам правил Лопиталя.
Правило Лопиталя для случая предела двух бесконечно малых величин. Пусть функции f(x) и g(x) имеют производные (то есть дифференцируемы) в некоторой окрестности точки a. А в самой точке a они могут и не иметь производных. При этом в окрестности точки a производная функции g(x) не равна нулю (g'(x)≠0) и пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны нулю:
.
Тогда предел отношения этих функций равен пределу отношения их производных:
.
Правило Лопиталя для случая предела двух бесконечно больших величин. Пусть функции f(x) и g(x) имеют производные (то есть дифференцируемы) в некоторой окрестности точки a. А в самой точке a они могут и не иметь производных. При этом в окрестности точки a производная функции g(x) не равна нулю (g'(x)≠0) и пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны бесконечности:
.
Тогда предел отношения этих функций равен пределу отношения их производных:
.
Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций равен пределу отношения их производных, если последний существует (конечный, то есть равный определённому числу, или бесконечный, то есть равный бесконечности).
Замечания.
1. Правила Лопиталя применимы и тогда, когда функции f(x) и g(x) не определены при x = a.
2. Если при вычисления предела отношения производных функций f(x) и g(x) снова приходим к неопределённости вида 0/0 или ∞/∞, то правила Лопиталя следует применять многократно (минимум дважды).
3. Правила Лопиталя применимы и тогда, когда аргумент функций (икс) стремится не к конечному числу a, а к бесконечности (x → ∞).
К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.
Пример 1. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
Решение. Подстановка в заданную функцию значения x=2 приводит к неопределённости вида 0/0. Поэтому производную каждой функции и получаем
В числителе вычисляли производную многочлена, а в знаменателе - производную сложной логарифмической функции. Перед последним знаком равенства вычисляли обычный предел, подставляя вместо икса двойку.
Пример 2. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
.
Решение. Подстановка в заданную функцию значения x=0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:
Пример 3. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
.
Решение. Подстановка в заданную функцию значения x=0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:
Пример 4. Вычислить
.
Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:
Замечание. Переходим к примерам, в которых правило Лопиталя приходится применять дважды, то есть приходить к пределу отношений вторых производных, так как предел отношения первых производных представляет собой неопределённость вида 0/0 или ∞/∞.
Пример 5. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
.
Решение. Находим
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных дают неопределённость вида ∞/∞.
Пример 6. Вычислить
.
Решение. Находим
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных дают неопределённость вида 0/0.
Пример 7. Вычислить
.
Решение. Находим
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных сначала дают неопределённость вида - ∞/∞, а затем неопределённость вида 0/0.
Пример 8. Вычислить
.
Решение. Находим
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных сначала дают неопределённость вида ∞/∞, а затем неопределённость вида 0/0.
Пример 11. Вычислить
.
Решение. Получаем
(здесь неопределённость вида 0∙∞ мы преобразовали к виду ∞/∞, так как
а затем применили правила Лопиталя).
Пример 12. Вычислить
.
Решение. Получаем
В этом примере использовано тригонометрическое тождество .
Неопределённости вида , или обычно приводятся к виду 0/0 или ∞/∞ с помощью логарифмирования функции вида
Чтобы вычислить предел выражения , следует использовать логарифмическое тождество , частным случаем которого является и свойство логарифма .
Используя логарифмическое тождество и свойство непрерывности функции (для перехода за знак предела), предел следует вычислять следующим образом:
Отдельно следует находить предел выражения в показателе степени и возводить e в найденную степень.
Пример 13. Вычислить, пользуясь правилом Лопиталя
.
Решение. Получаем
Вычисляем предел выражения в показателе степени
.
Итак,
.
Пример 14. Вычислить, пользуясь правилом Лопиталя
.
Решение. Получаем
Вычисляем предел выражения в показателе степени
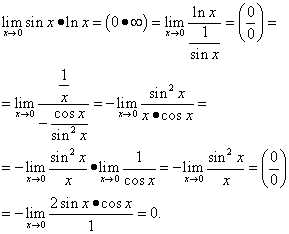 .
.
Итак,
.
Пример 15. Вычислить, пользуясь правилом Лопиталя
.
Решение. Получаем
Вычисляем предел выражения в показателе степени
Итак,
.
Это случаи, когда вычисление предела разности функций приводит к неопределённости "бесконечность минус бесконечность": .
Вычисление такого предела по правилу Лопиталя в общем виде выглядит следующим образом:
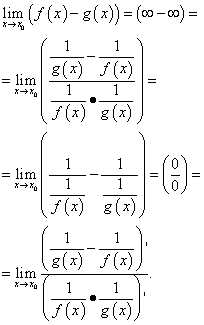
В результате таких преобразований часто получаются сложные выражения, поэтому целесообразно использовать такие преобразования разности функций, как приведение к общему знаменателю, умножение и деление на одно и то же число, использование тригонометрических тождеств и т.д.
Пример 16. Вычислить, пользуясь правилом Лопиталя
.
Решение. Пользуясь вышеперечисленными рекомендациями, получаем
Пример 17. Вычислить, пользуясь правилом Лопиталя
.
Решение. Пользуясь вышеперечисленными рекомендациями, получаем
Весь блок "Производная"
Правило Лопиталя · Калькулятор Онлайн
Введите функцию и точку для предела, которому надо применить правило Лопиталя
Вычислим предел функции с помощью правила Лопиталя. Вы введёте функцию, для которой требуется вычислить предел и точку в которой предел должен сходиться.
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция - арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция - арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- e
- e число, которое примерно равно 2.7
- exp(x)
- Функция - экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - pi
- Число - "Пи", которое примерно равно 3.14
- sin(x)
- Функция - Синус от x
- cos(x)
- Функция - Косинус от x
- sinh(x)
- Функция - Синус гиперболический от x
- cosh(x)
- Функция - Косинус гиперболический от x
- sqrt(x)
- Функция - квадратный корень из x
- sqr(x) или x^2
- Функция - Квадрат x
- tg(x)
- Функция - Тангенс от x
- tgh(x)
- Функция - Тангенс гиперболический от x
- cbrt(x)
- Функция - кубический корень из x
- Действительные числа
- вводить в виде 7.5, не 7,5
- 2*x
- - умножение
- 3/x
- - деление
- x^3
- - возведение в степень
- x + 7
- - сложение
- x - 6
- - вычитание
Другие функции:
- floor(x)
- Функция - округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция - округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция - Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
Правило Лопиталя — ПриМат
Метод нахождения пределов функций, раскрывающий неопределённости вида $latex \frac{0}{0} $ или $latex \frac{\infty}{\infty} $ Правило позволяет заменить предел отношения функций пределом отношения их производных.
1. Докажем теорему для случая, когда пределы функций равны нулю.
Условия:
- $latex f(x) &s=1$ и $latex g(x) &s=1$ дифференцируемы в проколотой окрестности точки $latex a $
- $latex \lim\limits_{x\to a}f(x)=\lim\limits_{x\to a}g(x)=0 &s=1$
- $latex g'(x) \neq 0 &s=1$ в проколотой окрестности точки $latex a $
- Существует $latex \lim\limits_{x\to a}\frac{f'(x)}{g'(x)} &s=1$
Вывод: Тогда существует $latex \lim\limits_{x \rightarrow a} \frac{f(x)}{g(x)} = \lim\limits_{x \rightarrow a} \frac{f'(x)}{g'(x)} &s=1$
Доказательство: Доопределим функции в точке $latex a $ нулём. Из 1 условия следует, что $latex f(x) $ и $latex g(x) $ непрерывны на отрезке $latex [a,x] $, где $latex x $ принадлежит рассматриваемой окрестности точки $latex a $. Применим обобщённую формулу конечных приращений (Коши) к $latex f(x) $ и $latex g(x) $ на отрезке $latex [a,x] $ $latex \exists \xi\in [a,x]:\frac{f(x)-f(a)}{g(x)-g(a)}=\frac{f'(\xi)}{g'(\xi)}&s=1 $ Так как $latex f(a)=g(a)=0 $ получим, что $latex \forall x $ $latex \exists \xi \in [a,x]:\frac{f(x)}{g(x)}=\frac{f'(\xi)}{g'(\xi)} &s=1$ Пусть предел отношения производных равен $latex A $. Следовательно: $latex \lim\limits_{x \to a} \frac{f'(\xi(x))}{g'(\xi(x))}=\lim\limits_{y \to a} \frac{f'(y)}{g'(y)}=A &s=1$, так как $latex \lim\limits_{x \to a} \xi(x)=a &s=1$
2. Докажем теорему для случая, когда пределы функций равны бесконечности.
Условия:
- $latex f(x) $ и $latex g(x) $ дифференцируемы при $latex x>a $
- $latex \lim\limits_{x\to\infty}f(x)=\lim\limits_{x\to\infty}g(x)=\infty &s=1$
- $latex g'(x)\neq 0 $ при $latex x>a $
- Существует конечный $latex \lim\limits_{x\to\infty}\frac{f'(x)}{g'(x)}=A &s=1$
Вывод: Тогда существует $latex \lim\limits_{x\to\infty}\frac{f(x)}{g(x)}=\lim\limits_{x\to\infty}\frac{f'(x)}{g'(x)} &s=1$ Доказательство: Из условия 2 следует, что $latex \exists a_{1}>a:\forall x>a_{1} \to |f(x)|>1,|g(x)|>1 $, и поэтому $latex f(x)\neq 0,g(x)\neq0 $ при $latex x>a_{1} $. По определению предела (условие 4) для заданного числа $latex \varepsilon >0 $ можно найти $latex \delta_{1}=\delta_{1}(\varepsilon)\geq a_{1} $ такое, что для всех $latex t>\delta_{1} $ выполняется неравенство: $latex A-\frac{\varepsilon}{2}<\frac{f'(t)}{g'(t)}<A+\frac{\varepsilon}{2} &s=1$ Фиксируя $latex x_{0}>\delta_{1} $ выберем, пользуясь условием 2 число $latex \delta_{2}>x_{0} $
такое, чтобы при всех $latex x>\delta_{2} $ выполнялись неравенства: $latex \left |\frac{f(x_{0})}{f(x)}<\frac{1}{2}\right | &s=1$ и $latex \left |\frac{g(x_{0})}{g(x)}<\frac{1}{2}\right | &s=1$ Для доказательства теоремы нужно доказать, что существует такое $latex \delta $, что при всех $latex x>\delta $ выполняется неравенство: $latex A-\varepsilon<\frac{f(x)}{g(x)}<A+\varepsilon (*) &s=1$ Число $latex \delta $ будет выбрано ниже. Считая, что $latex x>\delta $, применим к функциям $latex f $ и $latex g $ на отрезке $latex [x;x_{0}] $ обобщённую формулу конечных приращений (Коши). $latex \exists \xi \in [x_{0};x]: \frac{f(x)-f(x_{0})}{g(x)-g(x_{0})}=\frac{f'(\xi)}{g'(\xi)} &s=1$ Преобразуем левую часть неравенства: $latex \frac{f(x)-f(x_{0})}{g(x)-g(x_{0})}=\frac{f(x)}{g(x)}(\varphi(x))^{-1} &s=1$, где $latex \varphi(x)=\frac{1-\frac{g(x_{0})}{g(x)}}{1-\frac{f(x_{0})}{f(x)}}=1+\beta(x) &s=1$ Заметим, что $latex \beta(x)\to0 $ при $latex x\to+\infty $ в силу условия 2, поэтому $latex \forall \varepsilon>0 \exists \delta\geq\delta_{2}: $ $latex \forall x>\delta\to|\beta(x)|<\frac{\frac{\varepsilon}{2}}{|A|+ \frac{\varepsilon}{2}}(**) &s=1$ Так как $latex \xi>x_{0}>\delta_{1} $, то для всех $latex x>\delta_{2} $ выполняется неравенство: $latex A-\frac{\varepsilon}{2}<\frac{f(x)}{g(x)} (\varphi(x))^{-1}<A+\frac{\varepsilon}{2} &s=1$ Если $latex x>\delta $, то $latex \varphi(x)>0 $, и поэтому неравенство равносильно следующему: $latex (A-\frac{\varepsilon}{2})(1+\beta(x))< $ $latex \frac{f(x)}{g(x)}<(A+\frac{\varepsilon}{2})(1+\beta(x)) &s=1$ Используя неравенство $latex (**) $, получаем: $latex (A-\frac{\varepsilon}{2})(1+\beta(x))=$ $latex A-\frac{\varepsilon}{2}+(A-\frac{\varepsilon}{2})\beta(x) \geq $ $latex (A-\frac{\varepsilon}{2})-&s=1-(|A|+\frac{\varepsilon}{2})|\beta(x)|> $ $latex A-\frac{\varepsilon}{2}-\frac{\varepsilon}{2}=A-\varepsilon &s=1$ Аналогично находим: $latex (A+\frac{\varepsilon}{2})(1+\beta(x))\leq $ $latex A+\frac{\varepsilon}{2}+(|A|+\frac{\varepsilon}{2})|\beta(x)|< A+\varepsilon &s=1$
Таким образом для всех $latex x>\delta $ выполняется неравенство $latex (*) $, а это означает, что справедливо утверждение: $latex \lim\limits_{x\to\infty}\frac{f(x)}{g(x)}=\lim\limits_{x\to\infty}\frac{f'(x)}{g'(x)} &s=1$
Примеры:
Пример 1. Найти $latex \lim\limits_{x \to 1}\frac{3x^{10}-2x^{5}-1}{x^{3}-4x^{2}+3} &s=1$ Обозначим $latex f(x)=3x^{10}-2x^{5}-1 $ , $latex g(x)=x^{3}-4x^{2}+3 $. Так как $latex \lim\limits_{x\to1}f(x)=\lim\limits_{x\to1}g(x)=0 $, воспользуемся правилом Лопиталя для ситуации $latex \frac{0}{0} $. $latex f'(x)=30x^{9}-10x^{4} $, $latex f'(1)=20 $ $latex g'(x)=3x^{2}-8x $, $latex g'(1)=-5 $ По доказанной теореме: $latex \lim\limits_{x\to1}\frac{f(x)}{g(x)}=\lim\limits_{x\to1}\frac{f'(x)}{g(x’)}=\frac{20}{-5}=-4 &s=1$
Ответ: -4.
Пример 2. Доказать, что [latex] \lim\limits_{x\to\infty}\frac{\ln x}{x^{\alpha}}=0,\alpha>0 [/latex]
Применяя правило Лопиталя для ситуации $latex \frac{\infty}{\infty} $, получим: [latex]\lim\limits_{x\to\infty}\frac{\ln x}{x^{\alpha}}=[/latex][latex]\lim\limits_{x\to\infty}\frac{\frac{1}{x}}{\alpha x^{\alpha-1}}=[/latex][latex] \lim\limits_{x\to\infty}\frac{1}{\alpha x^{\alpha}}=0[/latex]
Доказано.
Источники:
- Конспект по курсу математического анализа Лысенко З.М.
- Тер-Крикоровв А.М., Шабунин М.И. Курс математического анализа -М.:ФИЗМАТ-ЛИТ, 2001.-672 с. гл. IV §19 с. 172-175
Тест на знание правила Лопиталя
Лимит времени: 0
Информация
Пройдите короткий тест для закрепления материала.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается...
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 10
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
Рубрики
- Математический анализ 0%
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
- С ответом
- С отметкой о просмотре
Поделиться ссылкой:
2.4.3. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ «Правило Лопиталя»
Задача 1.
Вычислить предел
Указание
Для того чтобы избавиться от неопределенности, примените правило Лопиталя:
Решение
Ответ:
Задача 2.
Вычислить предел
Указание
Для того чтобы избавиться от неопределенности, примените правило Лопиталя:
Если в результате вновь получится неопределенность, можно применять правило Лопиталя несколько раз.
Решение
Ответ: 3.
Задача 3.
Вычислить предел
Указание
Для того чтобы избавиться от неопределенности, примените правило Лопиталя:
Если в результате вновь получится неопределенность, можно применять правило Лопиталя несколько раз.
Решение
Ответ: 0.
Задача 4.
Вычислить предел
Указание
Преобразуйте функцию к виду
Тогда предел показателя степени можно вычислить по правилу Лопиталя.
Решение
Ответ: 1.
Задача 5.
Вычислить предел
Указание
Преобразуйте функцию, стоящую под знаком предела:
Решение
Ответ:
| < Предыдущая | Следующая > |
|---|
Правила Лопиталя | Математика, которая мне нравится
Швейцарский математик Иоганн I Бернулли (1667-1748) после успешного окончания Базельского университета, путешествуя по Европе, в 1690 году приезжает в Париж. В литературном салоне философа Никола Мальбранша (1638-1715) Иоганн знакомится с французским математиком маркизом Гийомом Франсуа Антуаном де Лопиталем (1661-1704). В ходе оживленной беседы Лопиталь удивился, как легко, “как бы играя”, юнец Бернулли решал трудные задачи по новому исчислению. Поэтому Лопиталь попросил прочитать ему несколько лекций. Устные беседы понравились Лопиталю, и он за приличный гонорар стал получать материалы в письменном виде. Заметим, что общеизвестное теперь “правило Лопиталя” для раскрытия неопределенностей также было передано ему Иоганном. Уже в 1696 году появился знаменитый трактат Лопиталя “Введение в анализ бесконечно малых для понимания кривых линий”. Вторая часть курса, изложенного Иоганном I Бернулли, была опубликована лишь в 1742 году и называлась “Математические лекции о методе интегралов и другие; написаны для знаменитого маркиза Госпиталия; годы 1691–1692”. В 1921 году были обнаружены рукописные копии лекций, написанные рукой Иоганна I Бернулли, оригиналы которых были переданы Лопиталю в 1691–1692 гг. Из них ученые неожиданно обнаружили, что Лопталь в своем “Анализе” почти не отступал от лекций своего молодого учителя.
Теорема (Коши). Пусть функции и непрерывны на , дифференцируемы на и . Тогда :
Доказательство. Рассмотрим функцию
выберем так, чтобы выполнялись все условия теоремы Ролля, т.е. .
По теореме Ролля существует :
Первое правило Лопиталя
Определение. Пусть функции , непрерывны на , дифференцируемы в , причем . Пусть . Тогда говорят, что отношение при представляет собой неопределенность вида .
Теорема. Если при указанных условиях существует
то и
Пусть конечно. По выберем : в интервале выполняется неравенство
Применим теорему Коши к отрезку , где . Существует :
и, значит,
Это и означает, что .
В случае, когда бесконечно, неравенство (1) заменяется на
или
в зависимости от знака . В остальном доказательство не меняется.
Второе правило Лопиталя
Определение. Пусть функции , непрерывны и дифференцируемы в , причем . Пусть . Тогда говорят, что отношение при представляет собой неопределенность вида .
Теорема. Если при указанных условиях существует
то и
Доказательство. Пусть конечно. По выберем : в интервале выполняется неравенство
Определим функцию из условия
Имеем
при . Применим к отрезку теорему Коши. Получим, что существует :
Для тех , для которых
Так как произвольно мало, то
В случае, когда , неравенство (2) заменяется на
а неравенство (4) — на неравенство
имеющим место при , достаточно близких к в силу (3).
Аналогично рассматривается случай .
Решение пределов по правилу Лопиталя
Метод решения
Одним из самых мощных методов раскрытия неопределенностей и вычисления пределов функций является использование правила Лопиталя. Оно позволяет раскрывать неопределенности вида 0/0 или ∞/∞ в конечной или бесконечно удаленной точке, которую мы обозначим как x0. Правило Лопиталя заключается в том, что мы находим производные числителя и знаменателя дроби. Если существует предел , то существует равный ему предел .
Если после дифференцирования мы опять получаем неопределенность, то процесс можно повторить, то есть применить правило Лопиталя уже к пределу . И так далее, до раскрытия неопределенности.
Для применения этого правила, должна существовать такая проколотая окрестность точки x0, на которой функции в числителе и знаменателе являются дифференцируемыми и функция в знаменателе и ее производная не обращается в нуль.
Применение правила Лопиталя состоит из следующих шагов.
1) Приводим неопределенность к виду 0/0 или ∞/∞. Для этого, если требуется, выполняем преобразования и делаем замену переменной. В результате получаем предел вида .
2) Убеждаемся, что существует такая проколотая окрестность точки x0, на которой функции в числителе и знаменателе являются дифференцируемыми и знаменатель и его производная не обращаются в нуль.
3) Находим производные числителя и знаменателя.
4) Если имеется конечный или бесконечный предел , то задача решена: .
5) Если предела не существует, то это не означает, что не существует исходного предела. Это означает, что данную задачу решить с помощью правила Лопиталя нельзя. Нужно применить другой метод (см. пример ниже).
6) Если в пределе вновь возникает неопределенность, то к нему также можно применить правило Лопиталя, начиная с пункта 2).
Как указывалось выше, применение правила Лопиталя может привести к функции, предела которой не существует. Однако это не означает, что не существует исходного предела. Рассмотрим следующий пример.
.
Применяем правило Лопиталя. , .
Однако предела не существует. Не смотря на это, исходная функция имеет предел:
.
Правило Лопиталя. Формулировки теорем
Здесь мы приводим формулировки теорем, на которых основывается раскрытие неопределенностей по правилу Лопиталя.
Теорема о раскрытии неопределенности 0/0
Пусть функции f и g имеют производные в проколотой (двусторонней или односторонней) окрестности конечной или бесконечно удаленной () точки , причем и не равны нулю в этой окрестности. И пусть
.
Тогда, если существует конечный или бесконечный предел
,
то существует равный ему предел
.
Здесь для двусторонней окрестности. Для односторонней окрестности, , или .
Теорема о раскрытии неопределенности ∞/∞
Пусть функции f и g имеют производные в проколотой (двусторонней или односторонней) окрестности конечной или бесконечно удаленной () точки , причем не равна нулю в этой окрестности. И пусть
.
Тогда, если существует конечный или бесконечный предел
,
то существует равный ему предел
.
Здесь для двусторонней окрестности. Для односторонней окрестности, , или .
Примеры
Все примеры Далее мы приводим подробные решения следующих пределов с помощью правила Лопиталя.
⇓, ⇓, ⇓,
⇓, ⇓, ⇓.
Пример 1
Все примеры ⇑ Показать, что экспонента растет быстрее любой степенной функции, а логарифм – медленнее. То есть показать, что
А) ;
Б) ,
где .
Решение
Рассмотрим предел А). При . Это неопределенность вида . Для ее раскрытия применим правило Лопиталя. Пусть
.
Находим производные. . Тогда
.
Если , то неопределенность исчезает, поскольку при . По правилу Лопиталя,
.
Если , то применяем правило Лопиталя n раз, где – целая часть числа b.
;
.
Поскольку , то . Хотя мы привыкли читать слева направо, но эту серию равенств следует читать справа налево следующим образом. Поскольку существует предел , то существует равный ему предел . Поскольку существует предел , то существует равный ему предел . И так далее, пока не дойдем до предела .
Теперь рассмотрим предел Б):
. Сделаем замену переменной . Тогда ; при ; .
Пример 2
Все примеры ⇑ Найти предел с помощью правила Лопиталя:
.
Решение
Это неопределенность вида 0/0. Находим по правилу Лопиталя.
.
Здесь, после первого применения правила мы снова получили неопределенность. Поэтому применили правило Лопиталя второй раз. Эту серию равенств нужно читать справа налево следующим образом. Поскольку существует предел , то существует равный ему предел . Поскольку существует предел , то существует равный ему исходный предел .
Ответ
Пример 3
Все примеры ⇑ Вычислить предел, используя правило Лопиталя.
.
Решение
Найдем значения числителя и знаменателя при :
;
.
Числитель и знаменатель равны нулю. Мы имеем неопределенность вида 0/0. Для ее раскрытия, применим правило Лопиталя.
.
Ответ
Пример 4
Все примеры ⇑ Решить предел с помощью правила Лопиталя.
.
Решение
Здесь мы имеем неопределенность вида (+0)+0. Преобразуем ее к виду +∞/+∞. Для этого выполняем преобразования.
.
Находим предел в показателе степени, применяя правило Лопиталя.
.
Поскольку экспонента – непрерывная функция для всех значений аргумента, то
.
Ответ
.
Пример 5
Все примеры ⇑ Найти предел используя правило Лопиталя:
.
Решение
Здесь мы имеем неопределенность вида ∞ – ∞. Приводя дроби к общему знаменателю, приведем ее к неопределенности вида 0/0:
.
Применяем правило Лопиталя.
;
;
.
Здесь у нас снова неопределенность вида 0/0. Применяем правило Лопиталя еще раз.
;
;
.
Окончательно имеем:
.
Как и во всех пределах, вычисляемых с помощью правила Лопиталя, читать нужно с конца. Поскольку существует предел , то существует равный ему предел . Поскольку существует предел , то существует равный ему исходный предел .
Можно упростить вычисления, если воспользоваться теоремой о замене функций эквивалентными в пределе частного. Согласно этой теореме, если функция является дробью или произведением множителей, то множители можно заменить на эквивалентные функции. Поскольку при , то
.
Ответ
Использованная литература:
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, 2003.
Автор: Олег Одинцов. Опубликовано:
Найдите ошибку: правило Лопиталя | Математика, которая мне нравится

Гийом Франсуа Лопиталь
Вот такой вот софизм. Математический анализ, правило Лопиталя. Думаю, многие хорошо его знают. В самом деле хорошо? Давайте посмотрим.
Требуется найти предел
Как видите, это неопределенность вида . Действуем по правилу Лопиталя и дифференцируем числитель и знаменатель. Получаем
И снова та же самая неопределенность . Что ж, применим снова правило Лопиталя и продифференцируем еще раз числитель и знаменатель. Наш исходный предел равен
И у нас получилось, что предела нет. Действительно, не имеет предела при .
Давайте вычислим теперь этот предел иначе. Представим дробь в виде суммы двух дробей, каждая из которых имеет предел:
Поскольку , а при неограниченно возрастает, то второе слагаемое равно нулю.
Итак, получилось, что исходный предел равен .
Получились противоречивые результаты. Хорошо, давайте проверим еще одним способом. Построим график функции :
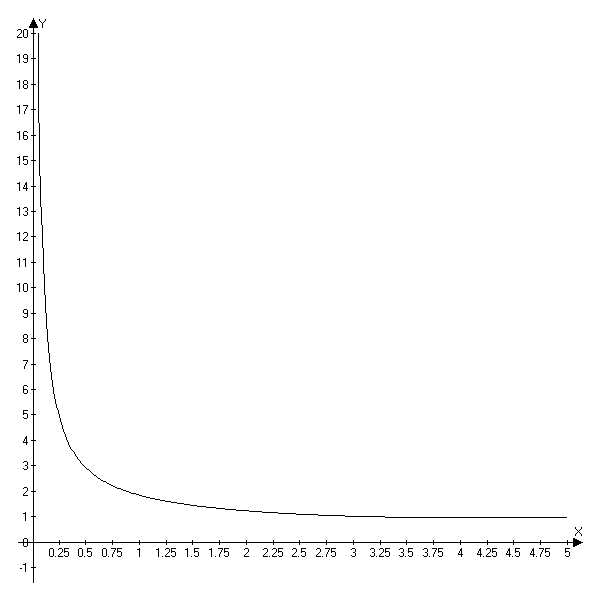
И похоже, что ответ правильный.
В чем же подвох?
Показать решение
В правиле Лопиталя ничего не говорится о существовании предела, если не существует предела отношения производных. Он может существовать, а может и не существовать.
Правило Лопиталя
Доказательство.
\(\circ\) Из условий \eqref{ref8} следует, что
$$
\exists\alpha_{1} > \alpha:\ \forall x > \alpha_{1}\rightarrow\ |f(x)| > 1,\ |g(x)| > 1,\label{ref11}
$$
и поэтому \(f(x)\neq 0,\ g(x)\neq 0\) при \(x > \alpha_1\). По определению предела \eqref{ref9} для заданного числа \(\varepsilon > 0\) можно найти \(\delta=\delta_1(\varepsilon)\geq \alpha_1\) такое, что для всех \(t > \delta_{1}\) выполняется неравенство
$$
A-\frac{\varepsilon}{2} < \frac{f'(t)}{g'(t)} < A+\frac{\varepsilon}{2}.\label{ref12}
$$
Фиксируя \(x_{0} > \delta_{1}\) (рис. 19.1), выберем, пользуясь условиями \eqref{ref8}, число \(\delta_{2} > x_{0}\) такое, чтобы при всех \(x > \delta_{2}\) выполнялись неравенства
$$
\left|\frac{f(x_{0})}{f(x)}\right| < \frac{1}{2},\quad \left|\frac{g(x_{0})}{g(x)}\right| < \frac{1}{2}.\label{ref13}
$$
Для доказательства утверждения \eqref{ref10} нужно показать, что существует \(\delta\) такое, что при всех \(x > \delta\) выполняется неравенство
$$
A-\varepsilon < \frac{f(x)}{g(x)} < A+\varepsilon.\label{ref14}
$$
Число \(\delta\) будет выбрано ниже. Считая, что \(x > \delta\), применим к функциям \(f\) и \(g\) на отрезке \([x_0,x]\) теорему Коши о среднем. В силу этой теоремы существует точка \(\xi\in [x_{0},x]\) такая, что
$$
\frac{f(x)-f(x_{0})}{g(x)-g(x_{0})}=\frac{f'(\xi)}{g'(\xi)}.\label{ref15}
$$
Преобразуем левую часть равенства \eqref{ref15}, используя условия \eqref{ref11} и \eqref{ref13}:
$$
\frac{f(x)-f(x_{0})}{g(x)-g(x_{0})}=\frac{f(x)}{g(x)}(\varphi(x))^{-1},\label{ref16}
$$
где
$$
\varphi(x)=\frac{1-g(x_0)/g(x)}{1-f(x_0)/f(x)}=1+\beta(x).\label{ref17}
$$
Заметим, что \(\beta(x)\rightarrow 0\) при \(x\rightarrow +\infty\) в силу условий \eqref{ref8}. Поэтому
$$
\forall \varepsilon > 0\ \exists\delta\geq\delta_{2}:\ \forall x > \delta\rightarrow|\beta(x)| < \frac{\varepsilon/2}{|A|+\varepsilon/2}.\label{ref18}
$$
Так как \(\xi > x_{0} > \delta_{1}\), то из равенств \eqref{ref16}, \eqref{ref17} и условия \eqref{ref12} следует, что для всех \(x > \delta_{2}\) выполняется неравенство
$$
A-\frac{\varepsilon}{2} < \frac{f(x)}{g(x)}(\varphi(x))^{-1} < A+\frac{\varepsilon}{2}.\label{ref19}
$$
Если \(x > \delta\), то \(\phi(x) > 0\) в силу условий \eqref{ref17} и \eqref{ref18}, и поэтому неравенство \eqref{ref19} равносильно следующему:
$$
(A-\frac{\varepsilon}{2})(1+\beta(x)) < \frac{f(x)}{g(x)} < (A+\frac{\varepsilon}{2})(1+\beta(x)).\label{ref20}
$$
Используя неравенство \eqref{ref18}, получаем
$$
(A-\frac{\varepsilon}{2})(1+\beta(x))=A-\frac{\varepsilon}{2}+\left(A-\frac{\varepsilon}{2}\right)\beta(x)\geq A-\frac{\varepsilon}{2}-\left(|A|+\frac{\varepsilon}{2}\right)|\beta(x)| > A-\frac{\varepsilon}{2}-\frac{\varepsilon}{2}=A-\varepsilon.\nonumber
$$
Аналогично находим
$$
\left(A+\frac{\varepsilon}{2}\right)(1+\beta(x)) \leq A+\frac{\varepsilon}{2}+\left(|A|+\frac{\varepsilon}{2}\right)|\beta(x)| < A+\varepsilon.\nonumber
$$
Таким образом, для всех \(x > \delta\) выполняется неравенство \eqref{ref14}. это означает, что справедливо утверждение \eqref{ref10}. \(\bullet\)
Правило Лопиталя — Википедия. Что такое Правило Лопиталя
Теорема Лопита́ля (также правило Бернулли — Лопиталя[1]) — метод нахождения пределов функций, раскрывающий неопределённости вида 0/0{\displaystyle 0/0} и ∞/∞{\displaystyle \infty /\infty }. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Содержание
- 1 Точная формулировка
- 2 История
- 3 Примеры
- 4 В искусстве
- 5 Примечания
Точная формулировка
Теорема Лопиталя:
Если:
- limx→af(x)=limx→ag(x)=0{\displaystyle \lim _{x\to a}{f(x)}=\lim _{x\to a}{g(x)}=0} или ∞{\displaystyle \infty };
- f(x){\displaystyle f(x)} и g(x){\displaystyle g(x)} дифференцируемы в окрестности a{\displaystyle a};
- g′(x)≠0{\displaystyle g'(x)\neq 0} в окрестности a{\displaystyle a};
- существует limx→af′(x)g′(x){\displaystyle \lim \limits _{x\to a}{\frac {f'(x)}{g'(x)}}},
то существует limx→af(x)g(x)=limx→af′(x)g′(x){\displaystyle \lim \limits _{x\to a}{\frac {f(x)}{g(x)}}=\lim \limits _{x\to a}{\frac {f'(x)}{g'(x)}}}.
Пределы также могут быть односторонними.
История
Способ раскрытия такого рода неопределённостей был опубликован в учебнике «Analyse des Infiniment Petits» 1696 года за авторством Гийома Лопиталя. Метод был сообщён Лопиталю в письме его первооткрывателем Иоганном Бернулли.[2]
Примеры
- limx→0x2+5x3x=limx→02x+53=53{\displaystyle \lim _{x\to 0}{\frac {x^{2}+5x}{3x}}=\lim _{x\to 0}{\frac {2x+5}{3}}={\frac {5}{3}}}
- limx→∞x3+4x2+7x+9x3+3x2=limx→∞3x2+8x+73x2+6x=limx→∞6x+86x+6=66=1{\displaystyle \lim _{x\to \infty }{\frac {x^{3}+4x^{2}+7x+9}{x^{3}+3x^{2}}}=\lim _{x\to \infty }{\frac {3x^{2}+8x+7}{3x^{2}+6x}}=\lim _{x\to \infty }{\frac {6x+8}{6x+6}}={\frac {6}{6}}=1}
Здесь можно применить правило Лопиталя 3 раза, а можно поступить иначе. Нужно разделить и числитель, и знаменатель на x{\displaystyle x} в наибольшей степени(в нашем случае x3{\displaystyle x^{3}}). В этом примере получается:- limx→∞1+4/x+7/x2+9/x31+3/x=11=1{\displaystyle \lim _{x\to \infty }{\frac {1+4/x+7/x^{2}+9/x^{3}}{1+3/x}}={\frac {1}{1}}=1}
- limx→+∞exxa=limx→+∞exa⋅xa−1=…=limx→+∞exa!=+∞{\displaystyle \lim _{x\to +\infty }{\frac {e^{x}}{x^{a}}}=\lim _{x\to +\infty }{\frac {e^{x}}{a\cdot x^{a-1}}}=\ldots =\lim _{x\to +\infty }{\frac {e^{x}}{a!}}=+\infty } — применение правила a{\displaystyle a} раз;
- limx→+∞xalnx=limx→+∞axa−11x=a⋅limx→+∞xa=+∞{\displaystyle \lim _{x\to +\infty }{\frac {x^{a}}{\ln {x}}}=\lim _{x\to +\infty }{\frac {ax^{a-1}}{\frac {1}{x}}}=a\cdot \lim _{x\to +\infty }{x^{a}}=+\infty } при a>0{\displaystyle a>0}.
В искусстве
…и рассказывали анекдоты о раскрытии неопределенностей методом Лопиталя
Братья Стругацкие, «Понедельник начинается в субботу».
А также песня группы «Научно-технический рэп» — «Правило Лопиталя».
Примечания
- ↑ http://lib.mexmat.ru/pr/matan_gavr_1.pdf
- ↑ Paul J. Nahin, An Imaginary Tale: The Story of −1{\displaystyle {\sqrt {-1}}}, p.216
Лопиталя правило - это... Что такое Лопиталя правило?
В математическом анализе правилом Лопита́ля называют метод нахождения пределов функций, раскрывающий неопределённости вида 0 / 0 и . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Точная формулировка
Правило говорит, что если функции f(x) и g(x) обладают следующим набором условий:
- или ;
- ;
- в проколотой окрестности a;
- Если g(x) и f(x) — дифференцируемы в проколотой окрестности a,
тогда существует . При этом теорема верна и для других баз (для указанной будет приведено доказательство).
История
Способ раскрытия такого рода неопределённостей был опубликован Лопиталем в его сочинении «Анализ бесконечно малых», изданном в 1696 году. В предисловии к этому сочинению Лопиталь указывает, что без всякого стеснения пользовался открытиями Лейбница и братьев Бернулли и «не имеет ничего против того, чтобы они предъявили свои авторские права на все, что им угодно». Иоганн Бернулли предъявил претензии на все сочинение Лопиталя целиком и в частности после смерти Лопиталя опубликовал работу под примечательным названием «Усовершенствование моего опубликованного в „Анализе бесконечно малых“ метода для определения значения дроби, числитель и знаменатель которой иногда исчезают», 1704.
Доказательство
Отношение бесконечно малых
Докажем теорему для случая, когда пределы функций равны нулю (т. н. неопределённость вида ).
Поскольку мы рассматриваем функции f и g только в правой проколотой полуокрестности точки a, мы можем непрерывным образом их доопределить в этой точке: пусть f(a) = g(a) = 0. Возьмём некоторый x из рассматриваемой полуокрестности и применим к отрезку теорему Коши. По этой теореме получим:
- ,
но f(a) = g(a) = 0, поэтому .
Дальше, записав определение предела отношения производных и обозначив последний через A, из полученного равенства выводим:
- для конечного предела и
- для бесконечного,
что является определением предела отношения функций.
Отношение бесконечно больших
Докажем теорему для неопределённостей вида .
Пусть, для начала, предел отношения производных конечен и равен A. Тогда, при стремлении x к a справа, это отношение можно записать как A + α, где α — O(1). Запишем это условие:
- .
Зафиксируем t из отрезка и применим теорему Коши ко всем x из отрезка :
- , что можно привести к следующему виду:
- .
Для x, достаточно близких к a, выражение имеет смысл; предел первого множителя правой части равен единице (так как f(t) и g(t) — константы, а f(x) и g(x) стремятся к бесконечности). Значит, этот множитель равен 1 + β, где β — бесконечно малая функция при стремлении x к a справа. Выпишем определение этого факта, используя то же значение , что и в определении для α:
- .
Получили, что отношение функций представимо в виде (1 + β)(A + α), и . По любому данному можно найти такое , чтобы модуль разности отношения функций и A был меньше , значит, предел отношения функций действительно равен A.
Если же предел A бесконечен (допустим, он равен плюс бесконечности), то
- .
В определении β будем брать ; первый множитель правой части будет больше 1/2 при x, достаточно близких к a, а тогда .
Для других баз доказательства аналогичны приведённым.
Примеры
Здесь можно применить правило Лопиталя 3 раза, а можно поступить иначе. Можно разделить и числитель, и знаменатель на x в наибольшей степени(в нашем случае x3). В этом примере получается:- ;
- при a > 0.
(Только если числитель и знаменатель ОБА стремятся или к 0; или к ; или к .)
Wikimedia Foundation. 2010.







